
【题目】如图1,在正方形ABCD中,P在对角线AC上,E在AC的延长线上,PB=PM , DE=EF.
(1)求证:∠CDE=∠F;
(2)若AB=5,CM=1,求PB的长;
(3)如图2,若BF=10,△QCF是以CF为底的等腰三角形,连接DQ , 试求△CDQ的最大面积.
【答案】
(1)
过E作EG⊥CF于G,EH⊥DC于H
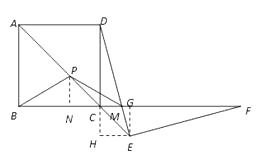
则四边形CHEG是矩形,
∵四边形ABCD是正方形,
∴∠ACB=∠ACD=45°,
∴∠ECG=∠ECH=45°,
∴CH=EH
∵矩形CHEG是正方形
∴EG=EH
又∵DE=EF,∴Rt△DEH≌Rt△FEG
∴∠CDE=∠F
(2)
解:过P作PN⊥BC于N
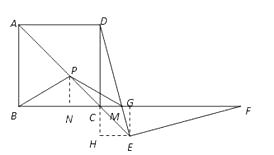
∵BC=AB=5,CM=1,∴BM=6
∵PB=PM,∴BN=NM=3,
∴NC=2
在Rt△PNC中,∵∠PCN=45°,
∴PN=NC=2
在Rt△PNM中,PM= ![]() =
= ![]() =
= ![]() ,
,
∴PB= ![]()
(3)
作QR⊥CF于R,QK⊥CD于K
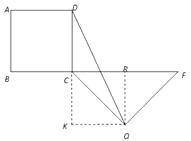
则四边形CKQR是矩形,
∴KQ=CR
又∵△QCF是以CF为底的等腰三角形,∴ CR=RF=![]() CF
CF
设BC=x,则CD=x,
KQ=CR=![]() CF=
CF=![]() (10-x)=5-
(10-x)=5-![]() x
x
∴S△CDQ=![]() CD·KQ=
CD·KQ=![]() ·x·(5-
·x·(5-![]() x)
x)
=-![]() x2+
x2+ ![]() x=-
x=-![]() (x-5)2+
(x-5)2+ ![]()
∴当x=5,△CDQ的面积有最大值 ![]()
【解析】
【考点精析】掌握等腰三角形的性质和勾股定理的概念是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】如图,在下列解答中,填写适当的理由或数学式:

(1)∵ ∠ABD=∠CDB, ( 已知 )
∴ ∥ . ( )
(2)∵ ∠ADC+∠DCB=180°, ( 已知 )
∴ ∥ . ( )
(3)∵ AD∥BE, ( 已知 )
∴ ∠DCE=∠ . ( )
(4)∵ ∥ , ( 已知 )
∴ ∠BAE=∠CFE. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是学习一元一次方程应用时,老师出示的问题和两名同学所列的方程,根据图中信息,解答下列问题.

(1)小杰同学所列方程中的x表示什么,小婷同学所列方程中的y表示什么;
(2)两个方程中任选一个,并写出它的等量关系;
(3)解(2)中你所选择的方程,并回答老师提出的问题。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
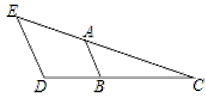
【题目】如图,∠E=50°,∠BAC=50°,∠D=110°,求∠ABD的度数.
请完善解答过程,并在括号内填写相应的理论依据.
解:∵∠E=50°,∠BAC=50°,(已知)
∴∠E= (等量代换)
∴ ∥ .( )
∴∠ABD+∠D=180°.( )
∴∠D=110°,(已知)
∴∠ABD=70°.(等式的性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么 ![]() 的值是 .
的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A. 
(1)求证:AC=AF;
(2)在边AB的下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,并证明四边形CDGB是矩形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com