
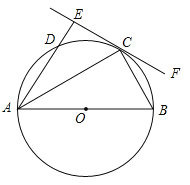
【题目】如图,AB为⊙O的直径,C、D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF⊥AD,交AD的延长线于点E,连接BC.
(1)求证:EF是⊙O的切线;
(2)若DE=1,BC=2,求劣弧![]() 的长l.
的长l.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,根据等腰三角形的性质得到∠OAC=∠DAC,求得∠DAC=∠OCA,推出AD∥OC,得到∠OCF=∠AEC=90°,于是得到结论;
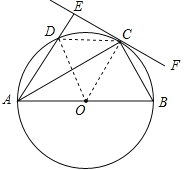
(2)连接OD,DC,根据角平分线的定义得到∠DAC=∠OAC,根据三角函数的定义得到∠ECD=30°,得到∠OCD=60°,得到∠BOC=∠COD=60°,OC=2,于是得到结论.
试题解析:(1)证明:连接OC,∵OA=OC,∴∠OAC=∠DAC,∴∠DAC=∠OCA,∴AD∥OC,∵∠AEC=90°,∴∠OCF=∠AEC=90°,∴EF是⊙O的切线;
(2)连接OD,DC,∵∠DAC=![]() ∠DOC,∠OAC=
∠DOC,∠OAC=![]() ∠BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=
∠BOC,∴∠DAC=∠OAC,∵ED=1,DC=2,∴sin∠ECD=![]() ,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l=
,∴∠ECD=30°,∴∠OCD=60°,∵OC=OD,∴△DOC是等边三角形,∴∠BOC=∠COD=60°,OC=2,∴l=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
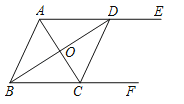
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将巧克力包装成方形、圆形礼盒出售,且每盒方形礼盒的价钱相同,每盒圆形礼盒的价钱相同.小明原先想购买3盒方形礼盒和7盒圆形礼盒,但他身上的钱还少240元,如果改成购买7盒方形礼盒和3盒圆形礼盒,他身上的钱会剩下240元.每盒圆形礼盒比每盒方形礼盒多( )
A.90元B.140元C.100元D.120元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式m2(a﹣2)+m(2﹣a)分解因式等于( )
A.(a﹣2)(m2+m)
B.(a﹣2)(m2﹣m)
C.m(a﹣2)(m﹣1)
D.m(a﹣2)(m+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 . 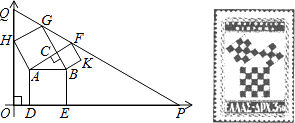
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com