
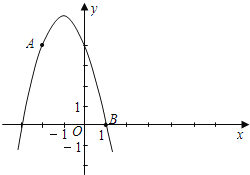
【题目】如图已知点A (﹣2,4)和点B (1,0)都在抛物线y=mx2+2mx+n上.
(1)求m、n;
(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;
(3)记平移后抛物线的对称轴与直线AB′的交点为点C,试在x轴上找点D,使得以点B′、C、D为顶点的三角形与△ABC相似.
【答案】(1)m=﹣![]() ,n=4 (2)y=﹣
,n=4 (2)y=﹣![]() (x﹣4)2+
(x﹣4)2+![]() (3)D(3,0)或(
(3)D(3,0)或(![]() ,0).
,0).
【解析】(1)已知了抛物线图象上A、B两点的坐标,将它们代入抛物线的解析式中,即可求得m、n的值.
(2)根据A、B的坐标,易求得AB的长;根据平移的性质知:四边形AA′B′B一定为平行四边形,若四边形AA′B′B为菱形,那么必须满足AB=BB′,由此可确定平移的距离,根据“左加右减”的平移规律即可求得平移后的抛物线解析式.
(3)易求得直线AB′的解析式,联立平移后的抛物线对称轴,可得到C点的坐标,进而可求出AB、BC、AC、B′C的长;在(2)题中已经证得AB=BB′,那么∠BAC=∠BB′C,即A、B′对应,若以点B′、C、D为顶点的三角形与△ABC相似,可分两种情况考虑:①∠B′CD=∠ABC,此时△B′CD∽△ABC,②∠B′DC=∠ABC,此时△B′DC∽△ABC;
根据上述两种不同的相似三角形所得不同的比例线段,即可求得不同的BD长,进而可求得D点的坐标.
解:(1)由于抛物线经过A (﹣2,4)和点B (1,0),则有:
![]() ,解得
,解得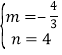 ;
;
故m=﹣![]() ,n=4.
,n=4.
(2)由(1)得:y=﹣![]() x2﹣
x2﹣![]() x+4=﹣
x+4=﹣![]() (x+1)2+
(x+1)2+![]() ;
;
由A (﹣2,4)、B (1,0),可得AB=![]() =5;
=5;
若四边形A A′B′B为菱形,则AB=BB′=5,即B′(6,0);
故抛物线需向右平移5个单位,即:
y=﹣![]() (x+1﹣5)2+
(x+1﹣5)2+![]() =﹣
=﹣![]() (x﹣4)2+
(x﹣4)2+![]() .
.
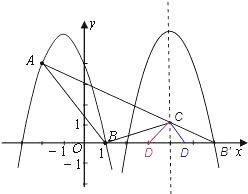
(3)由(2)得:平移后抛物线的对称轴为:x=4;
∵A(﹣2,4),B′(6,0),
∴直线AB′:y=﹣![]() x+3;
x+3;
当x=4时,y=1,故C(4,1);
所以:AC=3![]() ,B′C=
,B′C=![]() ,BC=
,BC=![]() ;
;
由(2)知:AB=BB′=5,即∠BAC=∠BB′C;
若以点B′、C、D为顶点的三角形与△ABC相似,则:
①∠B′CD=∠ABC,则△B′CD∽△ABC,可得:
![]() =
=![]() ,即
,即![]() =
=![]() ,B′D=3,
,B′D=3,
此时D(3,0);
②∠B′DC=∠ABC,则△B′DC∽△ABC,可得:
![]() =
=![]() ,即
,即![]() =
=![]() ,B′D=
,B′D=![]() ,
,
此时D(![]() ,0);
,0);
综上所述,存在符合条件的D点,且坐标为:D(3,0)或(![]() ,0).
,0).
“点睛”此题考查了二次函数解析式的确定、函数图象的平移、菱形的判定和性质、相似三角形的判定和性质等知识;(3)题中,在相似三角形的对应角和对应边不确定的情况下,一定要分类讨论,以免漏解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.

(1)已知点A的坐标为![]() .①在点
.①在点![]()
![]()
![]() 中,为点A的“等距点”的是________;②若点B的坐标为
中,为点A的“等距点”的是________;②若点B的坐标为![]() ,且A,B两点为“等距点”,则点B的坐标为________.
,且A,B两点为“等距点”,则点B的坐标为________.
(2)若![]()
![]() 两点为“等距点”,求k的值.
两点为“等距点”,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,线段AD=10cm,点B,C都是线段AD上的点,且AC=7cm,BD=4cm,若E,F分别是线段AB,CD的中点,求BC与EF的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个多边形的各边都相等,且各内角也都相等,那么这个多边形就叫做正多边形.如图,就是一组正多边形,观察每个正多边形中∠α的变化情况,解答下列问题:

(1)将下面的表格补充完整:
正多边形边数 | 3 | 4 | 5 | 6 | … | n |
∠α的度数 | 60° | 45° |
|
| … |
|
(2)根据规律,是否存在一个正多边形,其中的∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MAN=120°,AC平分∠MAN.
(1)在图1中,若∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
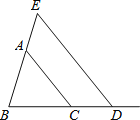
【题目】如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是 ;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两根木条,一根AB长为100cm,另一根CD长为150cm,在它们的中点处各有一个小圆孔MN(圆孔直径忽略不计,MN抽象成两个点),将它们的一端重合,放置在同一条直线上,此时两根木条的小圆孔之间的距离MN是____________cm.
![]()
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com