【题目】有两根木条,一根AB长为100cm,另一根CD长为150cm,在它们的中点处各有一个小圆孔MN(圆孔直径忽略不计,MN抽象成两个点),将它们的一端重合,放置在同一条直线上,此时两根木条的小圆孔之间的距离MN是____________cm.
科目：初中数学 来源： 题型：
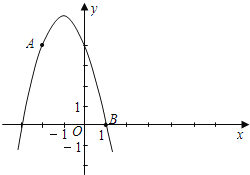
【题目】如图已知点A （﹣2，4）和点B （1，0）都在抛物线y=mx2+2mx+n上．
（1）求m、n；
（2）向右平移上述抛物线，记平移后点A的对应点为A′，点B的对应点为B′，若四边形A A′B′B为菱形，求平移后抛物线的表达式；
（3）记平移后抛物线的对称轴与直线AB′的交点为点C，试在x轴上找点D，使得以点B′、C、D为顶点的三角形与△ABC相似．
查看答案和解析>>
科目：初中数学 来源： 题型：
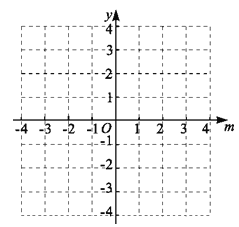
【题目】已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3=0 （m＞1）.
（1）求证：方程有两个不相等的实数根；
（2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；
（3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）.
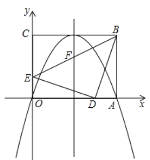
（1）求抛物线的解析式；
（2）猜想△EDB的形状并加以证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是以O为圆心，AB为直径的半圆上的动点，AB=6cm，设弦AP的长为xcm，△APO的面积为ycm2，（当点P与点A或点B重合时，y的值为0）．小明根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．下面是小明的探究过程，请补充完整；
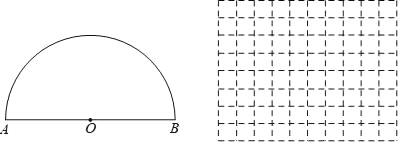
（1）通过取点、画图、测量、计算，得到了x与y的几组值，如下表：
x/cm | 0.5 | 1 | 2 | 3 | 3.5 | 4 | 5 | 5.5 | 5.8 |
y/cm2 | 0.8 | 1.5 | 2.8 | 3.9 | 4.2 | m | 4.2 | 3.3 | 2.3 |
那么m= ；（保留一位小数）
（2）建立平面直角坐标系，描出以表中各组对应值为坐标的点，画出该函数图象．
（3）结合函数图象说明，当△APO的面积是4时，则AP的值约为 ．（保留一位小数）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，把△ABC 先沿 x 轴翻折，再向右平移 3 个单位得到△A
BC 现把这两步 操作规定为一种变换．如图，已知等边三角形 ABC 的顶点 B、C 的坐标分别是（1，1）、（3，1）， 把三角形经过连续 5 次这种变换得到三角形△A
BC，则点 A 的对应点 A 的坐标是（ ）
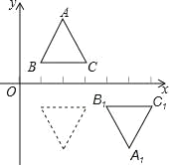
A.（5，﹣
）B.（14，1+）C.（17，﹣1﹣）D.（20，1+）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某巡警骑摩托车在一条南北大道上巡逻，某天他从岗亭出发，晚上停留在
处，规定向北方向为正，当天行驶纪录如下（单位：千米）
，
，
，
，
，
，
，
在岗亭何方？距岗亭多远？
在行驶过程中，最远处离出发点有多远？
若摩托车行驶
千米耗油
升，这一天共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】计算
（1）（-28）+37
（2）（-3）-1
（3）-49+91-5+（-9）
（4）12-（-18）+ （-7）-15
（5）
（6）23-17-（-7）+（-16）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，有一条线段AB，已知点A（﹣3，0）和B（0，4），平移线段AB得到线段A1B1．若点A的对应点A1的坐标为（0，﹣1），则线段AB平移经过的区域（四边形ABB1A1）的面积为（ ）
A. 12 B. 15 C. 24 D. 30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
