
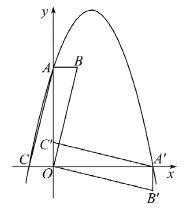
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.


【答案】(1)y=-x2+3x+4;(2)△AMA′的面积最大S△AMA′=8,M(2,6);(3)当P1(0,4),P2(3,4),P3(![]() ,-4),P4(
,-4),P4(![]() ,-4)时,P、N、B、Q构成平行四边形;当这个平行四边形为矩形时,N1(0,0),N2(3,0).
,-4)时,P、N、B、Q构成平行四边形;当这个平行四边形为矩形时,N1(0,0),N2(3,0).
【解析】试题分析:(1)先由OA′=OA得到点A′的坐标,再用点C、A、A′的坐标即可求此抛物线的解析式;(2)连接AA′, 过点M 作MN⊥x轴,交AA′于点N,把△AMA′分割为△AMN和△A′MN, △AMA′的面积=△AMA′的面积+△AMN的面积=![]() OA′MN,设点M的横坐标为x,借助抛物线的解析式和AA′的解析式,建立MN的长关于x的函数关系式,再据此建立△AMA′的面积关于x的二次函数关系式,再求△AMA′面积的最大值以及此时M的坐标;(3)在P、N、B、Q 这四个点中,B、Q 这两个点是固定点,因此可以考虑将BQ作为边、将BQ作为对角线分别构造符合题意的图形,再求解.
OA′MN,设点M的横坐标为x,借助抛物线的解析式和AA′的解析式,建立MN的长关于x的函数关系式,再据此建立△AMA′的面积关于x的二次函数关系式,再求△AMA′面积的最大值以及此时M的坐标;(3)在P、N、B、Q 这四个点中,B、Q 这两个点是固定点,因此可以考虑将BQ作为边、将BQ作为对角线分别构造符合题意的图形,再求解.
试题解析:(1)∵平行四边形ABOC绕点O顺时针旋转90°,得到平行四边形A′B′OC′,点A的坐标是(0,4),∴点A′的坐标为(4,0),点B的坐标为(1,4).
∵抛物线过点C,A,A′,设抛物线的函数解析式为y=ax2+bx+c(a≠0),可得:
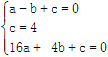 . 解得:
. 解得: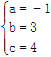 .∴抛物线的函数解析式为y=-x2+3x+4.
.∴抛物线的函数解析式为y=-x2+3x+4.
(2)连接AA′,设直线AA′的函数解析式为y=kx+b,可得
![]() .解得:
.解得:![]() .
.
∴直线AA'的函数解析式是y=-x+4.
设M(x,-x2+3x+4),
S△AMA′=![]() ×4×[-x2+3x+4一(一x+4)]=一2x2+8x=一2(x-2)2+8.
×4×[-x2+3x+4一(一x+4)]=一2x2+8x=一2(x-2)2+8.
∴x=2时,△AMA′的面积最大S△AMA′=8.
∴M(2,6).
(3)设P点的坐标为(x,-x2+3x+4),当P、N、B、Q构成平行四边形时,
①当BQ为边时,PN∥BQ且PN=BQ,
∵BQ=4,∴一x2+3x+4=±4.
当一x2+3x+4=4时,x1=0,x2=3,即P1(0,4),P2(3,4);
当一x2+3x+4=一4时,x3=![]() ,x4=
,x4=![]() ,即P3(
,即P3(![]() ,-4),P4(
,-4),P4(![]() ,-4);
,-4);
②当BQ为对角线时,PB∥x轴,即P1(0,4),P2(3,4);
当这个平行四边形为矩形时,即Pl(0,4),P2(3,4)时,N1(0,0),N2(3,0).
综上所述,当P1(0,4),P2(3,4),P3(![]() ,-4),P4(
,-4),P4(![]() ,-4)时,P、N、B、Q构成平行四边形;当这个平行四边形为矩形时,N1(0,0),N2(3,0).
,-4)时,P、N、B、Q构成平行四边形;当这个平行四边形为矩形时,N1(0,0),N2(3,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,直线EF分别与AB,CD交于点G,H,GM⊥EF,HN⊥EF,交AB于点N,∠1=50°. 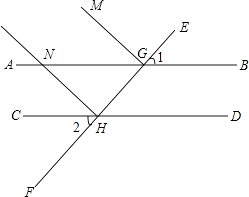
(1)求∠2的度数;
(2)试说明HN∥GM;
(3)∠HNG=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点是直线AB与x轴的正半轴,y轴的正半轴的交点,且OA,OB的长分别是x2﹣14x+48=0的两个根(OA>OB),射线BC平分∠ABO交x轴于C点,若有一动点P以每秒1个单位的速度从B点开始沿射线BC移动,运动时间为t秒.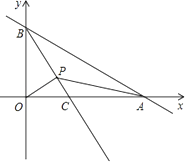
(1)求OA,OB的长;
(2)设△APB和△OPB的面积分别为s1 , s2 , 求s1:s2;
(3)在点P的运动过程中,△OPB可能是等腰三角形吗?若可能,直接写出时间t;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣1)2012+(π﹣3.14)0﹣(﹣ ![]() )﹣1;
)﹣1;
(2)![]() a2bc3(﹣2a2b2c)2;
a2bc3(﹣2a2b2c)2;![]()
(3)(4a3b﹣6a2b22ab)÷2ab;
(4)x2﹣(x+2)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中是常量,是变量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面几种三角形:
①有两个角为60°的三角形;
②三个外角都相等的三角形;
③一条边上的高也是这条边上的中线的三角形;
④有一个角为60°的等腰三角形.
其中是等边三角形的有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有员工50人,为了提高经济效益,决定引进一条新的生产线并从现有员工中抽调一部分员工到新的生产线上工作,经调查发现:分工后,留在原生产线上工作的员工每月人均产值提高40%;到新生产线上工作的员工每月人均产值为原来的3倍,设抽调x人到新生产线上工作.
(1)填空:若分工前员工每月的人均产值为a元,则分工后,留在原生产线上工作的员工每月人均产值是元,每月的总产值是元;到新生产线上工作的员工每月人均产值是元,每月的总产值是元;
(2)分工后,若留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值;而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半.问:抽调的人数应该在什么范围?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com