
【题目】林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中是常量,是变量.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某平行四边形的一条边长为12cm,则它的两条对角线长可以为( )
A.6cm,12cm
B.18cm,20cm
C.34cm,10cm
D.10cm,14cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
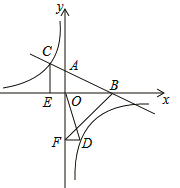
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种进价为20元/个的水杯,其销售量y(万个)与销售价格x(元/个)的变化如下表,销售过程中的其他开支(不含成本)总计40万元.
价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)求出该公司销售这种水杯的净利润z(万元)与销售价格x(元/个)的函数关系式,并求出销售价格定为多少时净利润最大?最大值是多少?
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把多项式m2(a-2)+m(2-a)分解因式,结果正确的是( )
A. m(a-2)(m+1) B. m(a-2)(m-1) C. m(2-a)(m-1) D. m(2-a)(m+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),
则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得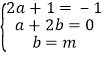 , 解得
, 解得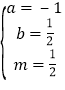 , ∴
, ∴![]()
解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取![]() ,
,
2×![]() =0,故
=0,故 ![]() .
.
(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com