
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
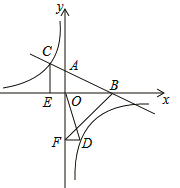
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
【答案】(1)y=-![]() ;(2)D(
;(2)D(![]() ,一4).
,一4).
【解析】
试题分析:(1)先由tan∠ABO=![]() =
=![]() 及OB=4,OE=2求出CE的长度,从而得到点C的坐标,再将点C的坐标代入y=
及OB=4,OE=2求出CE的长度,从而得到点C的坐标,再将点C的坐标代入y=![]() 即可求得反比例函数的解析式.(2)先由反比例函数y=
即可求得反比例函数的解析式.(2)先由反比例函数y=![]() 的k的几何意义得出S△DFO,由S△BAF=4S△DFO得到S△BAF,根据S△BAF=
的k的几何意义得出S△DFO,由S△BAF=4S△DFO得到S△BAF,根据S△BAF=![]() AFOB得出AF的长度,用AF-OA求出OF的长,据此可先得出点D的纵坐标,再求D得横坐标.
AFOB得出AF的长度,用AF-OA求出OF的长,据此可先得出点D的纵坐标,再求D得横坐标.
试题解析:(l)∵OB=4,OE=2,∴BE=OB+OE=6.
∵CE⊥x轴,∴∠CEB=90°.
在Rt△BEC中,∵tan∠ABO=![]() ,∴
,∴![]() =
=![]() .即
.即![]() =
=![]() ,解得CE=3.
,解得CE=3.
结合图象可知C点的坐标为(一2,3),
将C(―2,3)代入反比例函数解析式可得3=![]() .解得m=-6.
.解得m=-6.
反比例函数解析式为y=-![]() .
.
(2)解:方法一:∵点D是y=-![]() 的图象上的点,且DF⊥y轴,
的图象上的点,且DF⊥y轴,
∴S△DFO=![]() ×|-6|=3.
×|-6|=3.
∴S△BAF=4S△DFO=4×3=12.∴![]() AFOB=12.∴
AFOB=12.∴![]() ×AF×4=12.
×AF×4=12.
∴AF=6.∴EF=AF-OA=6-2=4.
∴点D的纵坐标为-4.
把y=-4代入y=-![]() ,得 -4=-
,得 -4=-![]() .∴x=
.∴x=![]() .
.
∴D(![]() ,一4).
,一4).
方法二:设点D的坐标为(a,b).
∵S△BAF=4S△DFO,∴![]() AFOB=4×
AFOB=4×![]() OFFD.∴(AO+OF) OB=4OFFD.
OFFD.∴(AO+OF) OB=4OFFD.
∴[2+(-b)]×4=-4ab.∴8-4b=-4ab.
又∵点D在反比例函数图象上,∴b=-![]() .∴ab=-6.∴8-4b=24.解得:b=-4.
.∴ab=-6.∴8-4b=24.解得:b=-4.
把b=-4代ab=-6中,解得:a=![]() .
.
∴D(![]() ,一4).
,一4).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形. 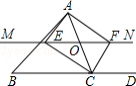
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.在数轴上表示-a的点一定在原点的左边
B.有理数a的倒数是
C.一个数的相反数一定小于或等于这个数
D.如果一个数的绝对值等于这个数的相反数,那么这个数是负数或零
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A、二元一次方程只有一个解
B、二元一次方程组有无数个解
C、二元一次方程组的解必是它所含的二元一次方程的解
D、三元一次方程组一定由三个三元一次方程组成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(﹣1)2012+(π﹣3.14)0﹣(﹣ ![]() )﹣1;
)﹣1;
(2)![]() a2bc3(﹣2a2b2c)2;
a2bc3(﹣2a2b2c)2;![]()
(3)(4a3b﹣6a2b22ab)÷2ab;
(4)x2﹣(x+2)(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列因式分解正确的是( )
A. 2x2-2=2(x+1)(x-1) B. x2+2x-1=(x-1)2
C. x2+1=(x+1)2 D. x2-x+2=x(x-1)+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】林老师骑摩托车到加油站加油,发现每个加油器上都有三个量,其中一个表示“元/升”其数值固定不变的,另外两个量分别表示“数量”、“金额”,数值一直在变化,在这三个量当中是常量,是变量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,点A、C的坐标分别为A(3,0),C(0,2),点B在第一象限. 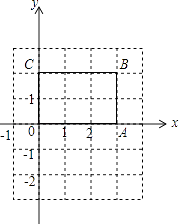
(1)写出点B的坐标;
(2)若过点C的直线交长方形的OA边于点D,且把长方形OABC的周长分成2:3的两部分,求点D的坐标;
(3)如果将(2)中的线段CD向下平移3个单位长度,得到对应线段C′D′,在平面直角坐标系中画出△CD′C′,并求出它的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com