【题目】如图，把六张大小完全相同的小长方形卡片（如图①）不重叠无缝隙的放在一个底面为长方形（长为
，宽为
）的盒子底部（如图②），盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长之和是（ ）
A.
B.
C.
D.
快乐小博士巩固与提高系列答案科目：初中数学 来源： 题型：
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇，下表是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
（进价、售价均保持不变，利润=销售收入﹣进货成本）
（1）求A、B两种型号的电风扇的销售单价；
（2）若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？
（3）在（2）的条件下，商场销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△BAC中，∠BAC=90°，将△ABC绕点A顺时针旋转90°得到△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′，若∠CC′B′=30°，求∠B的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）若AC=6，BC=8，OA=2，求线段DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：正方形ABCD，E为平面内任意一点，连接DE，将线段DE绕点D顺时针旋转90°得到DG，连接EC，AG．
（1）当点E在正方形ABCD内部时，
①根据题意，在图1中补全图形；
②判断AG与CE的数量关系与位置关系并写出证明思路．
（2）当点B，D，G在一条直线时，若AD＝4，DG＝
，求CE的长．（可在备用图中画图）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解题：据专家预测今年受厄尔尼诺现象影响，我国大部分地区可能遇到洪涝灾害．进入防汛期前，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话：
“你们是用9天完成4800米长的大坝加固任务的”？
“我们加固600米后采用新的加固模式，这样每天加固长度是原来的2倍”，
通过这段对话请你求出该地驻军原来每天加固的米数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作
APCD，AC与PD相交于点E，已知∠ABC=∠AEP=
(0°<<90°).
(1)求证: ∠EAP=∠EPA;
(2)APCD是否为矩形?请说明理由;
(3)如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系，并证明你的结论.
查看答案和解析>>
科目：初中数学 来源： 题型：
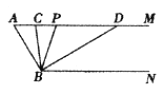
【题目】如图，已知AM//BN，∠A=600.点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D.
(1)①∠ABN的度数是 ；②∵AM //BN，∴∠ACB=∠ ；
(2)求∠CBD的度数；
(3)当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时，∠ABC的度数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
