
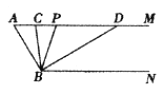
【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
【答案】(1)①120°;②∠CBN;(2)60°;(3)答案见解析;(4)30°.
【解析】
(1)①根据两直线平行,同旁内角互补即可求得答案;
②根据两直线平行,内错角相等即可得答案;
(2)由(1)知∠ABP+∠PBN=120°,继而结合角平分线的定义可得2∠CBP+2∠DBP=120°,进而可求得答案;
(3)由AM∥BN得∠APB=∠PBN、∠ADB=∠DBN,根据BD平分∠PBN知∠PBN=2∠DBN,从而可得∠APB:∠ADB=2:1;
(4)由AM∥BN得∠ACB=∠CBN,当∠ACB=∠ABD时有∠CBN=∠ABD,得∠ABC+∠CBD=∠CBD+∠DBN,即∠ABC=∠DBN,根据∠ABN=120°,∠CBD=60°可得答案.
(1)①∵AM∥BN,∠A=60°,
∴∠A+∠ABN=180°,
∴∠ABN=120°;
②∵AM∥BN,
∴∠ACB=∠CBN,
故答案为:①120°;②∠CBN;
(2)∵AM∥BN,
∴∠ABN+∠A=180°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°,
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°;
(3)不变,∠APB:∠ADB=2:1.
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB:∠ADB=2:1;
(4)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN,
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°,
故答案为:30°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,把六张大小完全相同的小长方形卡片(如图①)不重叠无缝隙的放在一个底面为长方形(长为![]() ,宽为
,宽为![]() )的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长之和是( )
)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长之和是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动.给出以下四个结论:

①AE=AF;
②∠CEF=∠CFE;
③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形;
④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.
上述结论中正确的序号有 .(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上.若点
轴的正半轴上.若点![]() ,
,![]() 在线段
在线段![]() 上,且
上,且![]() 为某个一边与
为某个一边与![]() 轴平行的矩形的对角线,则称这个矩形为点
轴平行的矩形的对角线,则称这个矩形为点![]() 、
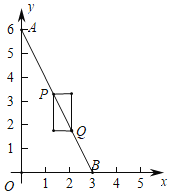
、![]() 的“涵矩形”.下图为点
的“涵矩形”.下图为点![]() ,
,![]() 的“涵矩形”的示意图.
的“涵矩形”的示意图.
(1)点![]() 的坐标为
的坐标为![]() .
.
①若点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 与点
与点![]() 重合,则点
重合,则点![]() 、
、![]() 的“涵矩形”的周长为__________.
的“涵矩形”的周长为__________.
②若点![]() ,
,![]() 的“涵矩形”的周长为
的“涵矩形”的周长为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“涵矩形”的顶点的是_________.
的“涵矩形”的顶点的是_________.
(2)四边形![]() 是点
是点![]() 、
、![]() 的“涵矩形”,点
的“涵矩形”,点![]() 在
在![]() 的内部,且它是正方形.
的内部,且它是正方形.
①当正方形![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 时,求点的坐标.
时,求点的坐标.
②当正方形![]() 的对角线长度为
的对角线长度为![]() 时,连结
时,连结![]() .直接写出线段
.直接写出线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是 ______ ,∠COD的余角是 ______
(2)OE是∠BOC的平分线吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖市拟建立了一个学生身份识别系统.利用图 1 的二维码可以进行身份识别,图2是某个学生的识别图案,黑色小正方形表示 1,白色小正方形表示 0.将第一行数字从左到 右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为 0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,请问,表示10班学生的识别图案是( )

A. B.
B.
C. D.
D.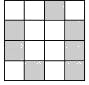
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
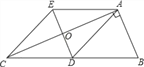
【题目】如图,在Rt△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连结EC.
(1)求证:AD=EC;
(2)求证:四边形ADCE是菱形;
(3)若AB=AO,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
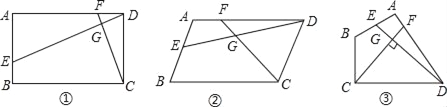
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且ADDF=AEDC,求证:DE⊥CF:
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DECD=CFDA:
(3)如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断![]() 是否为定值,并证明.
是否为定值,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com