
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上.若点
轴的正半轴上.若点![]() ,
,![]() 在线段
在线段![]() 上,且
上,且![]() 为某个一边与
为某个一边与![]() 轴平行的矩形的对角线,则称这个矩形为点
轴平行的矩形的对角线,则称这个矩形为点![]() 、
、![]() 的“涵矩形”.下图为点
的“涵矩形”.下图为点![]() ,
,![]() 的“涵矩形”的示意图.
的“涵矩形”的示意图.
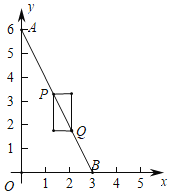
(1)点![]() 的坐标为
的坐标为![]() .
.
①若点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 与点
与点![]() 重合,则点
重合,则点![]() 、
、![]() 的“涵矩形”的周长为__________.
的“涵矩形”的周长为__________.
②若点![]() ,
,![]() 的“涵矩形”的周长为
的“涵矩形”的周长为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“涵矩形”的顶点的是_________.
的“涵矩形”的顶点的是_________.
(2)四边形![]() 是点
是点![]() 、
、![]() 的“涵矩形”,点
的“涵矩形”,点![]() 在
在![]() 的内部,且它是正方形.
的内部,且它是正方形.
①当正方形![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 时,求点的坐标.
时,求点的坐标.
②当正方形![]() 的对角线长度为
的对角线长度为![]() 时,连结
时,连结![]() .直接写出线段
.直接写出线段![]() 的取值范围.
的取值范围.
【答案】(1)①![]() . ②
. ②![]() ;(2)①点
;(2)①点![]() 的坐标为
的坐标为![]() 或
或![]() .②
.②![]() .
.
【解析】
(1)①利用A、B的坐标求出直线AB的解析式,再将P点横坐标代入,计算即可得点![]() 、
、![]() 的“新矩形”的周长;②由直线AB的解析式判定是否经过E、F、G三点,发现只经过了F(1,2),能够成为点
的“新矩形”的周长;②由直线AB的解析式判定是否经过E、F、G三点,发现只经过了F(1,2),能够成为点![]() 、
、![]() 的“涵矩形”的顶点的是F(1,2)
的“涵矩形”的顶点的是F(1,2)
(2)①①根据正方形的性质可得出∠ABO=45°,结合点A的坐标可得出点B的坐标及直线AB的函数表达式,由![]() 的横坐标为
的横坐标为![]() ,可得出点P的坐标,再由正方形的周长可得出点Q的坐标,进而可得出点Q的坐标;②由正方形的对角线长度为
,可得出点P的坐标,再由正方形的周长可得出点Q的坐标,进而可得出点Q的坐标;②由正方形的对角线长度为![]() ,可得正方形的边长为1,由直线AB的解析式y=-x+6可知M点的运动轨迹是直线y=-x+5,由点
,可得正方形的边长为1,由直线AB的解析式y=-x+6可知M点的运动轨迹是直线y=-x+5,由点![]() 在
在![]() 的内部,x的取值范围是0<x<5,OM<5,OM最小值是由O向直线y=-x+5作垂线段,此时OM=
的内部,x的取值范围是0<x<5,OM<5,OM最小值是由O向直线y=-x+5作垂线段,此时OM=![]() ,可得OM的取值范围.
,可得OM的取值范围.
(1)①解:由A(0,6),B(3,0)可得直线AB的解析式为:y=-2x+6,
∵P点横坐标是![]()
∴当x=![]() 时,y=3
时,y=3
∴P(![]() ,3).
,3).
∵ 点![]() 与点
与点![]() 重合,
重合,
∴Q(3,0)
∴点![]() 、
、![]() 的“涵矩形”的宽为:3-
的“涵矩形”的宽为:3-![]() =
=![]() ,长为3-0=3
,长为3-0=3
∴点![]() 、
、![]() 的“涵矩形”的周长为:
的“涵矩形”的周长为:![]()
故答案为:9
②.由①可得直线AB的解析式为:y=-2x+6可设Q(a,-2a+6),则成为点![]() 、
、![]() 的“涵矩形”的顶点且在
的“涵矩形”的顶点且在![]() AOB内部的一点坐标为M(1,-2a+6)
AOB内部的一点坐标为M(1,-2a+6)
∴PM=4-(-2a+6)=2a-2,MQ=a-1
∵点![]() ,
,![]() 的“涵矩形”的周长为
的“涵矩形”的周长为![]()
∴PM+MQ=3
∴2a-2+a-1=3
解得:a=2
∴M(1,2)
故答案为:F(1,2),只写![]() 或
或![]() 也可以.
也可以.
(2)①![]() 点
点![]() 、
、![]() 的“涵矩形”是正方形,
的“涵矩形”是正方形,
![]()
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 的坐标为 ,
的坐标为 ,
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 正方形
正方形![]() 的周长为
的周长为![]() ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②∵正方形的对角线长度为![]() ,
,
∴可得正方形的边长为1,
因为直线AB的解析式y=-x+6可设M点的运动轨迹是直线y=-x+b,且过(0,5)
故M点的运动轨迹是直线y=-x+5
∵点![]() 在
在![]() 的内部,x的取值范围是0<x<5,
的内部,x的取值范围是0<x<5,
∴当M落在OB或者OA边上时,OM取得最大值,此时OM=5,由于点![]() 在
在![]() 的内部,
的内部,
∴OM<5,
当OM⊥直线y=-x+5时,OM取得最小值,此时OM=![]() ,
,
∴OM的取值范围.![]() .
.
故答案为:![]()


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作![]() APCD,AC与PD相交于点E,已知∠ABC=∠AEP=
APCD,AC与PD相交于点E,已知∠ABC=∠AEP=![]() (0°<
(0°<![]() <90°).
<90°).
(1)求证: ∠EAP=∠EPA;
(2)![]() APCD是否为矩形?请说明理由;
APCD是否为矩形?请说明理由;
(3)如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:4x2y﹣[2xy2﹣3(xy2﹣x2y)+x2y]﹣5xy2,其中x=![]() ,y=1;
,y=1;
(2)当x=3时,代数式px3+qx+1的值等于2019;那么当x=﹣3时,求px3+qx+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向南骑行2km到达A村,继续向南骑行3km到达B 村,然后向北骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向北方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每100km耗油2升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
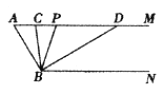
【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-20)+(+3)+(-5)+(+7);
(2)16-(-15)-4+(-5);
(3)(-12)×(-37)×![]() ;
;
(4)(-![]() )÷
)÷![]() ÷(-
÷(-![]() );
);
(5)-30×(![]()
![]()
![]() );
);
(6)-3-[-5 +(1-![]() ×0.6)÷(-3)]
×0.6)÷(-3)]
(7)![]()
(8)![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com