
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;

【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+3;(2)
x+3;(2)![]()
【解析】(1)由点C的坐标以及tan∠OAC=![]() .可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;
.可得出点A的坐标,结合点A、C的坐标利用待定系数法即可求出抛物线的解析式;
(2)设直线AC的解析式为y=kx+b,由点A、C的解析式利用待定系数法即可求出直线AC的解析式,设N(x,0)(-4<x<0),可找出H、P的坐标,由此即可得出PH关于x的解析式,利用配方法即二次函数的性质即可求出最值.
解:(1)∵C(0,3),
∴OC=3,
∵tan∠OAC=![]() ,
,
∴OA=4,
∴A(﹣4,0).
把A(﹣4,0)、C(0,3)代入y=ax2+2ax+c中,
得![]() ,
,
解得: 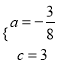 ,
,
∴抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+3.
x+3.
(2)设直线AC的解析式为y=kx+b,
把A(﹣4,0)、C(0,3)代入y=kx+b中,
得: ![]() ,
,
解得: 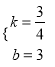 ,
,
∴直线AC的解析式为y=![]() x+3.
x+3.
设N(x,0)(﹣4<x<0),
则H(x, ![]() x+3),P(x,﹣
x+3),P(x,﹣![]() x2﹣
x2﹣![]() x+3),
x+3),
∴PH=﹣![]() x2﹣
x2﹣![]() x+3﹣(
x+3﹣(![]() x+3)=﹣
x+3)=﹣![]() x2﹣
x2﹣![]() x=﹣
x=﹣![]() (x+2)2+
(x+2)2+![]() ,
,
∵﹣![]() <0,
<0,
∴PH有最大值,
即当x=﹣2时,PH取最大值,最大值为![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:初中数学 来源: 题型:
【题目】根据要求完成画图或作答:
如图所示,已知点![]() 、
、![]() 、
、![]() 是网格纸上的三个格点.
是网格纸上的三个格点.

(1)画射线![]() ,画线段
,画线段![]() ,过点
,过点![]() 画
画![]() 的平行线
的平行线![]() ;
;
(2)过点![]() 画直线
画直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,则点
,则点![]() 到
到![]() 的距离就是线段_________的长度.
的距离就是线段_________的长度.
(3)线段![]() _______线段
_______线段![]() (填“
(填“![]() ”或“
”或“![]() ”),理由是_____________.
”),理由是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上.若点
轴的正半轴上.若点![]() ,
,![]() 在线段
在线段![]() 上,且
上,且![]() 为某个一边与
为某个一边与![]() 轴平行的矩形的对角线,则称这个矩形为点
轴平行的矩形的对角线,则称这个矩形为点![]() 、
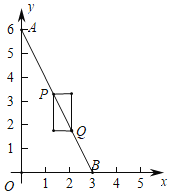
、![]() 的“涵矩形”.下图为点
的“涵矩形”.下图为点![]() ,
,![]() 的“涵矩形”的示意图.
的“涵矩形”的示意图.
(1)点![]() 的坐标为
的坐标为![]() .
.
①若点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 与点
与点![]() 重合,则点
重合,则点![]() 、
、![]() 的“涵矩形”的周长为__________.
的“涵矩形”的周长为__________.
②若点![]() ,
,![]() 的“涵矩形”的周长为
的“涵矩形”的周长为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() ,
,![]() ,
,![]() 中,能够成为点
中,能够成为点![]() 、
、![]() 的“涵矩形”的顶点的是_________.
的“涵矩形”的顶点的是_________.
(2)四边形![]() 是点
是点![]() 、
、![]() 的“涵矩形”,点
的“涵矩形”,点![]() 在
在![]() 的内部,且它是正方形.
的内部,且它是正方形.
①当正方形![]() 的周长为
的周长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 时,求点的坐标.
时,求点的坐标.
②当正方形![]() 的对角线长度为
的对角线长度为![]() 时,连结
时,连结![]() .直接写出线段
.直接写出线段![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芜湖市拟建立了一个学生身份识别系统.利用图 1 的二维码可以进行身份识别,图2是某个学生的识别图案,黑色小正方形表示 1,白色小正方形表示 0.将第一行数字从左到 右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为 0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,请问,表示10班学生的识别图案是( )

A. B.
B.
C. D.
D.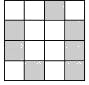
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点坐标为(3,3),将△ABC 先向下平移4个单位得△A'B'C',再将△A'B'C'绕点O逆时针旋转180°得△A'B'C'.
(1)请你画出△A'B'C'和△A'B'C';
(2)点A'的坐标为 ;
(3)△ABC和△A'B'C'关于某个点中心对称,这个点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
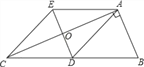
【题目】如图,在Rt△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连结EC.
(1)求证:AD=EC;
(2)求证:四边形ADCE是菱形;
(3)若AB=AO,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生,每年的4月23日被联合国教科文组织确定为“世界读书日”.蓝天中学为了解八年级学生本学期的课外阅读情况,随机抽查部分学生对其课外阅读量进行统计分析,绘制成两幅不完整的统计图.根据图示信息,解答下列问题:
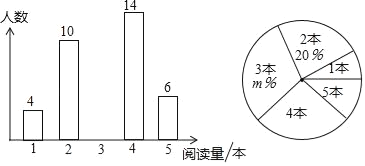
(1)求被抽查学生人数,课外阅读量的众数,扇形统计图中m的值;并将条形统计图补充完整;
(2)若规定:本学期阅读3本以上(含3本)课外书籍者为完成目标,据此估计该校600名学生中能完成此目标的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以矩形ABCD两对角线的交点O为原点建立平面直角坐标系,且x轴过BC中点,y轴过CD中点,y=![]() x﹣2与边AB、BC分别交于点E、F.若AB=10,BC=3,则△EBF的面积是( )
x﹣2与边AB、BC分别交于点E、F.若AB=10,BC=3,则△EBF的面积是( )
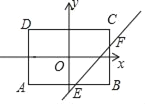
A. 4B. 5C. 6D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com