
【题目】以矩形ABCD两对角线的交点O为原点建立平面直角坐标系,且x轴过BC中点,y轴过CD中点,y=![]() x﹣2与边AB、BC分别交于点E、F.若AB=10,BC=3,则△EBF的面积是( )
x﹣2与边AB、BC分别交于点E、F.若AB=10,BC=3,则△EBF的面积是( )
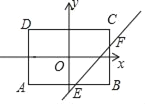
A. 4B. 5C. 6D. 7
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax+c交x轴于A,B两点,交y轴于点C(0,3),tan∠OAC=![]() .
.
(1)求抛物线的解析式;
(2)点H是线段AC上任意一点,过H作直线HN⊥x轴于点N,交抛物线于点P,求线段PH的最大值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-20)+(+3)+(-5)+(+7);
(2)16-(-15)-4+(-5);
(3)(-12)×(-37)×![]() ;
;
(4)(-![]() )÷
)÷![]() ÷(-
÷(-![]() );
);
(5)-30×(![]()
![]()
![]() );
);
(6)-3-[-5 +(1-![]() ×0.6)÷(-3)]
×0.6)÷(-3)]
(7)![]()
(8)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含有45°角的直角三角板ABC和直尺如图摆放在桌子上,然后分别过A、B两个顶点向直尺作两条垂线段AD,BE.
(1)请写出图中的一对全等三角形并证明;
(2)你能发现并证明线段AD,BE,DE之间的关系吗?
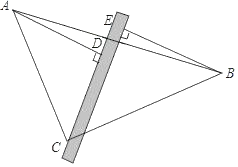
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②b2>4,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0.其中正确结论的个数是( )
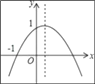
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰三角形,且AC=BC,∠ACB=120°,在AB上取一点O,使OB=OC,以点O为圆心,OB为半径作圆,过点C作CD∥AB交⊙O于点D,连接BD.
(1)猜想AC与⊙O的位置关系,并证明你的猜想;
(2)试判断四边形BOCD的形状,并证明你的判断;
(3)已知AC=6,求扇形OBC所围成的圆锥的底面圆的半径r.
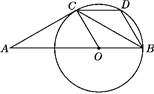
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图![]() ,
,![]() 分别为数轴上的两点,
分别为数轴上的两点,![]() 点对应的数为-10,
点对应的数为-10,![]() 点对应的数为90.
点对应的数为90.

(1)![]() ,
,![]() 两点间的距离为________.
两点间的距离为________.
(2)现在有一只电子蚂蚁![]() 从
从![]() 点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁
点出发,以2个单位/秒的速度向右运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以3个单位/秒的速度向左运动.运动时间为
点出发,以3个单位/秒的速度向左运动.运动时间为![]() 秒,用含
秒,用含![]() 的代数式表示:
的代数式表示:
①点![]() 在数轴上表示的数为________.
在数轴上表示的数为________.
②若两只电子蚂蚁在数轴上的![]() 点相遇,则
点相遇,则![]() 点对应的数是多少.
点对应的数是多少.
(3)若当电子蚂蚁![]() 从
从![]() 点出发时,以4个单位/秒的速度向左运动,同时另一只电子蚂蚁
点出发时,以4个单位/秒的速度向左运动,同时另一只电子蚂蚁![]() 恰好从
恰好从![]() 点出发,以6个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距20个单位长度.
点出发,以6个单位/秒的速度向左运动,经过多长的时间两只电子蚂蚁在数轴上相距20个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
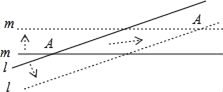
【题目】根据爱因斯坦的相对论可知,任何物体的运动速度不能超过光速(3×105km/s),因为一个物体达到光速需要无穷多的能量,并且时光会倒流,这在现实中是不可能的.但我们可让一个虚拟物超光速运动,例如:直线l,m表示两条木棒相交成的锐角的度数为10°,它们分别以与自身垂直的方向向两侧平移时,它们的交点A也随着移动(如图箭头所示),如果两条直线的移动速度都是光速的0.2倍,则交点A的移动速度是光速的_____倍.(结果保留两个有效数字).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com