
����Ŀ����ͼ(1),����ABC��,AB=BC,PΪAB����һ��,����CP,��PA��PCΪ�ڱ���![]() APCD��AC��PD�ཻ�ڵ�E����֪��ABC=��AEP=
APCD��AC��PD�ཻ�ڵ�E����֪��ABC=��AEP=![]() (0��<
(0��<![]() <90��).
<90��).
(1)��֤: ��EAP=��EPA;
(2)![]() APCD�Ƿ�Ϊ����?��˵������;
APCD�Ƿ�Ϊ����?��˵������;
(3)��ͼ(2),FΪBC�е�,����FP,����AEP�Ƶ�E˳ʱ����ת�ʵ��ĽǶ�,�õ���MEN(��M��N�ֱ�����MEN��������BA��FP�ӳ��ߵĽ���).�����߶�EM��EN֮���������ϵ����֤����Ľ���.

���𰸡�(1)��������
(2)![]() APCD�Ǿ���.�����ɼ�������
APCD�Ǿ���.�����ɼ�������
(3)EM=EN�����ɼ�����.
��������
��1������AB=BC��֤��CAB=��ACB��������ABC����AEP�У��������Ƕ�Ӧ��ȣ������������ڽǺͶ���������֤�ã�
��2���ɣ�1��֪��EPA=��EAP����AC=DP�����ݶԽ�����ȵ�ƽ���ı����Ǿ��μ�����֤��
��3������֤����EAM�ա�EPN���Ӷ��õ�EM=EN��
֤����(1)����ABC����AEP��,
![]() ��ABC=��AEP,��BAC=��EAP,
��ABC=��AEP,��BAC=��EAP,
![]() ��ACB=��APE,
��ACB=��APE,
����ABC��,AB=BC.![]() ��ACB=��BAC,
��ACB=��BAC,
![]() ��EPA=��EAP,
��EPA=��EAP,
(2)![]() APCD�Ǿ���.
APCD�Ǿ���.
![]() �ı���APCD��ƽ���ı���,
�ı���APCD��ƽ���ı���,
![]() AC=2EA,PD=2EP.
AC=2EA,PD=2EP.
��(1)֪, ��EPA=��EAP.
![]() EA=EP������AC=PD
EA=EP������AC=PD
![]()
![]() APCD�Ǿ���.
APCD�Ǿ���.
(3)EM=EN
![]() EA=EP,
EA=EP,![]() ��EPA=90�� -
��EPA=90�� -![]()
![]() ��EAM=180��-��EAP =180��-��EPA= 180��-(90��-
��EAM=180��-��EAP =180��-��EPA= 180��-(90��-![]() )=90��+
)=90��+![]()
��(2)֪, ��CPB=90��,F��BC���е�,![]() FP=FB,
FP=FB,
![]() ��FPB=��ABC=
��FPB=��ABC=![]() ��
��
![]() ��EPN=��EPA+��APN=��EPA+��FPB=90�� -
��EPN=��EPA+��APN=��EPA+��FPB=90�� -![]() +
+![]() =90��+
=90��+![]()
![]() ��EAM=��EPN
��EAM=��EPN
![]() ��AEP�Ƶ�E˳ʱ����ת�ʵ��ĽǶȣ��õ���MEN��
��AEP�Ƶ�E˳ʱ����ת�ʵ��ĽǶȣ��õ���MEN��
![]() ��AEP-��AEN =��MEN-��AEN,����MEA=��NEP.
��AEP-��AEN =��MEN-��AEN,����MEA=��NEP.
![]() ��EAM�ա�EPN,
��EAM�ա�EPN,
![]() EM=EN.
EM=EN.


 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�����Լ���ѧ·�ߵij��Ƚ�����20�β������õ�20������x1��x2������x20����֪x1+x2+��+x20��2019��������ʽ��x��x1��2+��x��x2��2+��+��x��x20��2ȡ����Сֵʱ��x��ֵΪ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������Ŵ�С��ȫ��ͬ��С�����ο�Ƭ����ͼ�٣����ص���϶�ķ���һ������Ϊ�����Σ���Ϊ![]() ����Ϊ
����Ϊ![]() ���ĺ��ӵײ�����ͼ�ڣ������ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ����������Ӱ���ֵ��ܳ�֮���ǣ� ��
���ĺ��ӵײ�����ͼ�ڣ������ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ����������Ӱ���ֵ��ܳ�֮���ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ҫ����ɻ�ͼ������
��ͼ��ʾ����֪��![]() ��
��![]() ��
��![]() ������ֽ�ϵ��������.
������ֽ�ϵ��������.

��1��������![]() �����߶�
�����߶�![]() ������
������![]() ��
��![]() ��ƽ����
��ƽ����![]() ��
��
��2������![]() ��ֱ��
��ֱ��![]() �Ĵ��ߣ�����Ϊ��
�Ĵ��ߣ�����Ϊ��![]() �����
�����![]() ��
��![]() �ľ�������߶�_________�ij���.
�ľ�������߶�_________�ij���.
��3���߶�![]() _______�߶�
_______�߶�![]() ������
������![]() ������
������![]() ������������_____________.
������������_____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����ι㳡��Ϊa�ף���Ϊb�ף��㳡���м�Բ���̵صİ뾶Ϊ![]() �ף��㳡�����Ƕ���һ��뾶��ͬ���ķ�֮һԲ�ε��̵أ���Բ���̵صİ뾶ҲΪ
�ף��㳡�����Ƕ���һ��뾶��ͬ���ķ�֮һԲ�ε��̵أ���Բ���̵صİ뾶ҲΪ![]() �ף�
�ף�

��1�����ô���ʽ�ֱ��ʾ�̵ص�������Ϳյص�������������������
��2���������γ�Ϊ500�ף���Ϊ300�ף���㳡�յص����������ȡ3.14��������������Ч��ѧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������A��B��C��D�ĸ�������![]() ���������ʾ����
���������ʾ����![]() ����
����![]() ����A��D�����ʾ�����ķֱ�Ϊ
����A��D�����ʾ�����ķֱ�Ϊ![]() ��6����EΪBD���е㣬��ô���������������������ʾ�������У����߶�BD���е������������
��6����EΪBD���е㣬��ô���������������������ʾ�������У����߶�BD���е������������![]() ����
����![]()
![]()
A. ![]() B. 0C. 1D. 2
B. 0C. 1D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���B=60�㣬��E��F�ֱ�ӵ�B��D������ͬ�����ٶ��ر�BC��DC���C�˶������������ĸ����ۣ�

��AE=AF��
����CEF=��CFE��
�۵���E��F�ֱ�Ϊ��BC��DC���е�ʱ����AEF�ǵȱ������Σ�
�ܵ���E��F�ֱ�Ϊ��BC��DC���е�ʱ����AEF��������
������������ȷ������� ����������Ϊ��ȷ����Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() �����������.����
�����������.����![]() ��
��![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() Ϊij��һ����
Ϊij��һ����![]() ��ƽ�еľ��εĶԽ��ߣ�����������Ϊ��
��ƽ�еľ��εĶԽ��ߣ�����������Ϊ��![]() ��
��![]() ������������.��ͼΪ��
������������.��ͼΪ��![]() ��
��![]() ��������������ʾ��ͼ.
��������������ʾ��ͼ.
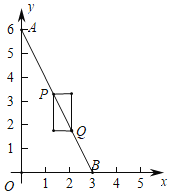
��1����![]() ������Ϊ
������Ϊ![]() .
.
������![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ����
����![]() ���
���![]() �غϣ����
�غϣ����![]() ��
��![]() ���������������ܳ�Ϊ__________.
���������������ܳ�Ϊ__________.
������![]() ��
��![]() ���������������ܳ�Ϊ
���������������ܳ�Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() �����
�����![]() ��
��![]() ��
��![]() �У��ܹ���Ϊ��
�У��ܹ���Ϊ��![]() ��
��![]() �������������Ķ������_________.
�������������Ķ������_________.
��2���ı���![]() �ǵ�
�ǵ�![]() ��
��![]() ����������������
����������������![]() ��
��![]() ���ڲ���������������.
���ڲ���������������.
�ٵ�������![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ʱ����������.
ʱ����������.
�ڵ�������![]() �ĶԽ��߳���Ϊ
�ĶԽ��߳���Ϊ![]() ʱ������
ʱ������![]() .ֱ��д���߶�
.ֱ��д���߶�![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
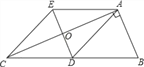
����Ŀ����ͼ����Rt��ABC�У�AD�DZ�BC�ϵ����ߣ�����A��AE��BC������D��DE��AB��DE��AC��AE�ֱ��ڵ�O����E������EC��
��1����֤��AD=EC��
��2����֤���ı���ADCE�����Σ�
��3����AB=AO����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com