
【题目】已知:二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3).
(1)求此二次函数的表达式,并用配方法将其化为y=a(x﹣h)2+k的形式;
(2)画出此函数图象的示意图.
【答案】(1)y=﹣(x﹣2)2+1;(2)见解析
【解析】
试题分析:(1)先将点(﹣1,﹣8),(0,﹣3)代入y=﹣x2+bx+c,列出关于b、c的二元一次方程组,求解得出b、c的值,得到二次函数的表达式,再用配方法化为顶点式的形式
(2)利用描点法画出函数图象即可.
解:(1)∵二次函数y=﹣x2+bx+c的图象过点(﹣1,﹣8),(0,﹣3),
∴![]() ,解得
,解得![]() ,
,
∴此二次函数的表达式为y=﹣x2+4x﹣3;
y=﹣x2+4x﹣3=﹣(x﹣2)2+1;
(2)∵y=﹣(x﹣2)2+1,
∴顶点坐标为(2,1),对称轴方程为x=2.
∵函数二次函数y=﹣x2+4x﹣3的开口向下,顶点坐标为(2,1),与x轴的交点为(3,0),(1,0),
∴其图象为



科目:初中数学 来源: 题型:
【题目】说明:从(A),(B)两题中任选一题做答.
春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
我选择:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则ABCD的周长为( )
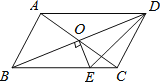
A.8cm B.12cm C.16cm D.24cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设[x]表示不超过x的最大整数,如[2.7] =2,[-4.5] =-5;计算[3.7] + [-6.5] 的值为( )
A.-2 B.-3C.-4D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com