Question

【题目】如图，在平面直角坐标系xOy中，点A在y轴上，点B在x轴上，∠ABO=60°，若点D（1，0）且BD=2OD．把△ABO绕着点D逆时针旋转m°（0＜m＜180）后，点B恰好落在初始Rt△ABO的边上，此时的点B记为B′，则点B′的坐标为 ．

Answer 1

【答案】（2，）或（0，）．

【解析】

试题分析：分类讨论：当点B恰好落在AB上，如图1，根据旋转的性质得DB=DB′=2，易得△DBB′为等边三角形，作B′E⊥DB于E，如图1，根据等边三角形的性质得DE=BE=BD=1，B′E=DE=，则B′（2，）；当点B恰好落在OA上，如图1，根据旋转的性质得DB=DB′=2，利用勾股定理计算出OB′=，则B′（0，），于是得到B′点的坐标为（2，）或（0，）．

解：∵点D（1，0）且BD=2OD，

∴BD=2，

当把△ABO绕着点D逆时针旋转m°（0＜m＜180）后得到△A′B′C′，点B恰好落在AB上，如图1，

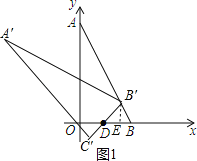
∴DB=DB′，

而∠ABO=60°，

∴△DBB′为等边三角形，

作B′E⊥DB于E，如图1，

∴DE=BE=BD=1，B′E=DE=，

∴B′（2，）；

当把△ABO绕着点D逆时针旋转m°（0＜m＜180）后得到△A′B′C′，点B恰好落在OA上，如图2，

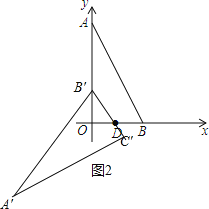
∴DB=DB′=2，

∴OB′==，

∴B′（0，）．

故答案为（2，）或（0，）．