
【题目】操作实践
(1)操作1:将矩形ABCD沿对角线AC折叠(如图1),猜想重叠部分是什么图形?并验证你的猜想.连结BE与AC有什么位置关系?
(2)操作2:折叠矩形ABCD,让点B落在对角线AC上(如图2),若AD=4,AB=3,请求出线段CE的长度.

【答案】(1)△AFC是等腰三角形.(2)CE=2.5.
【解析】
试题分析:(1)由矩形的性质可知AD∥BC,从而得到∠FAC=∠ACB,由翻折的性质可知∠ACB=∠ACF,于是得到∠FAC=∠FCA,故此可得到△AFC为等腰三角形;
(2)先依据勾股定理求得AC=5,由翻折的性质可知BE=EF,AF=AB=3,可求得FC=2,设EC=x,则BE=EF=4﹣x,最后在△EFC中由勾股定理可求得EC的长.
解:(1)∵四边形ABCD为矩形,
∴AD∥BC.
∴∠FAC=∠ACB.
由翻折的性质可知;∠ACB=∠ACF,
∴∠FAC=∠FCA.
∴AF=FC.
∴△AFC是等腰三角形.
(2)在Rt△ABC中,由勾股定理得:AC=![]() =5.
=5.
∵由翻折的性质可知:BE=EF,AF=AB=3.
∴FC=2,设EC=x,则BE=EF=4﹣x.
在Rt△EFC中,由勾股定理可知;EF2+FC2=EC2,即(x﹣4)2+22=x2.
解得:x=2.5.
∴CE=2.5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数y=![]() 的图象过点A(1,6).
的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数y=![]() 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B在x轴上,∠ABO=60°,若点D(1,0)且BD=2OD.把△ABO绕着点D逆时针旋转m°(0<m<180)后,点B恰好落在初始Rt△ABO的边上,此时的点B记为B′,则点B′的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O点是学校所在位置,A村位于学校南偏东42°方向,B村位于学校北偏东25°方向,C村位于学校北偏西65°方向,在B村和C村间的公路OE(射线)平分∠BOC.
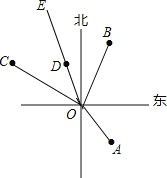
(1)求∠AOE的度数;
(2)公路OE上的车站D相对于学校O的方位是什么?(以正北、正南方向为基准)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com