
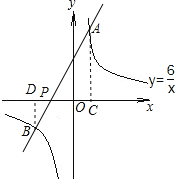
【题目】在平面直角坐标系xOy中,反比例函数y=![]() 的图象过点A(1,6).
的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数y=![]() 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
【答案】(1)y=![]() ;(2)P(﹣1,0).
;(2)P(﹣1,0).
【解析】
试题分析:(1)把A点代入,根据待定系数法即可求得;
(2)作AC⊥x轴于C,BD⊥x轴于D,通过证得△APC∽△BPD,得出![]() =
=![]() =2,求得B的纵坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令y=0,即可求得P的坐标.
=2,求得B的纵坐标,代入解析式求得坐标,然后根据待定系数法求得直线AB的解析式,令y=0,即可求得P的坐标.
解:(1)∵反比例函数y=![]() 的图象过点A(1,6),
的图象过点A(1,6),
∴k=1×6=6,
∴反比例函数的表达式为:y=![]() ;
;
(2)作AC⊥x轴于C,BD⊥x轴于D,
∵AC∥BD,
∴△APC∽△BPD,
∴![]() =
=![]() ,
,
∵AP=2PB,
∴AC=2BD,
∵AC=6,
∴BD=3,
∴B的纵坐标为﹣3,
代入y=![]() 得,﹣3=
得,﹣3=![]() ,解得x=﹣2,
,解得x=﹣2,
∴B(﹣2,﹣3),
设直线AB的解析式为y=kx+b,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=3x+3,
令y=0,则求得x=﹣1,
∴P(﹣1,0).


科目:初中数学 来源: 题型:
【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和哥哥在离家2千米的同一所学校上学,哥哥以4千米/时的速度步行去学校,小亮因找不到书籍耽误了15分钟,而后骑自行车以12千米/时的速度去追哥哥.
(1)到校前小亮能追上哥哥吗?
(2)如果小亮追上哥哥,此时离学校有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在争创全国卫生城市的活动中,某市“青年突击队’决定义务清运一堆重达100吨的垃圾,在清运了25吨后,由于周围居民的加入,使清运的速度比原来提高了一倍,结果仅用了5小时就完成了本次清运工作,青年突击队原来每小时清运多少吨垃圾?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作实践
(1)操作1:将矩形ABCD沿对角线AC折叠(如图1),猜想重叠部分是什么图形?并验证你的猜想.连结BE与AC有什么位置关系?
(2)操作2:折叠矩形ABCD,让点B落在对角线AC上(如图2),若AD=4,AB=3,请求出线段CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOM的平分线,OD是∠BOM的平分线.
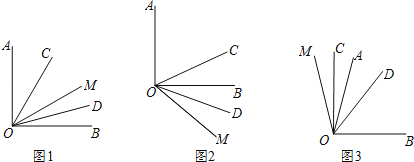
(1)如图1,若∠AOB=90°,∠AOM=60°,求∠COD的度数;
(2)如图2,若∠AOB=90°,∠AOM=130°,则∠COD= °;
(3)如图3,若∠AOB=m°,∠AOM=n°,则∠COD= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先观察,再解答.
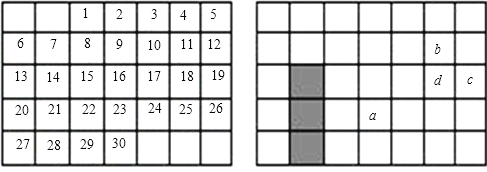
如图(1)是生活中常见的月历,你对它了解吗?
(1)图(2)是另一个月的月历,a表示该月中某一天,b、c、d是该月中其它3天,b、c、d与a有什么关系?b= ;c= ;d= .(用含a的式子填空).
(2)用一个长方形框圈出月历中的三个数字(如图3﹣2﹣2 (2)中的阴影),如果这三个数字之和等于51,这三个数字各是多少?
(3)这样圈出的三个数字的和可能是64吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com