
【题目】如图,OA⊥OB,AB⊥x轴于C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.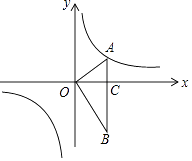
(1)求反比例函数y= ![]() 的表达式;
的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP= ![]() S△AOB , 求点P的坐标.
S△AOB , 求点P的坐标.
【答案】
(1)
解:把A( ![]() ,1)代入反比例函数y=
,1)代入反比例函数y= ![]() 得:k=1×
得:k=1× ![]() =
= ![]() ,
,
所以反比例函数的表达式为y= ![]() ;
;
(2)
解:∵A( ![]() ,1),OA⊥AB,AB⊥x轴于C,
,1),OA⊥AB,AB⊥x轴于C,
∴OC= ![]() ,AC=1,
,AC=1,
OA= ![]() =
= ![]() =2,
=2,
∵tanA= ![]() =
= ![]() ,
,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC﹣2 ![]() ,
,
∴S△AOB= ![]() =
= ![]() =2
=2 ![]() ,
,
∵S△AOP= ![]() S△AOB,
S△AOB,
∴ ![]() ,
,
∵AC=1,
∴OP=2 ![]() ,
,
∴点P的坐标为(﹣2 ![]() ,0).
,0).
【解析】(1)把A的坐标代入反比例函数的解析式,即可求出答案;(2)求出∠A=60°,∠B=30°,求出线段OA和OB,求出△AOB的面积,根据已知S△AOP= ![]() S△AOB , 求出OP长,即可求出答案.
S△AOB , 求出OP长,即可求出答案.
【考点精析】关于本题考查的比例系数k的几何意义,需要了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能得出正确答案.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.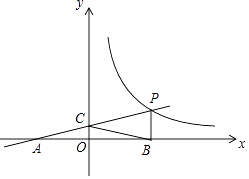
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.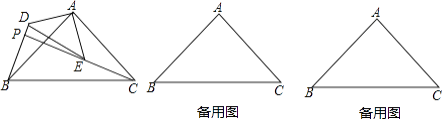
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
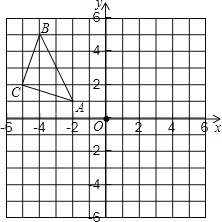
【题目】操作探究:如图,△ABC在平面直角坐标系中,其中,点A,B,C的坐标分别为A(–2,1),B(–4,5),C(–5,2).
(1)作△ABC关于直线l:x=–1对称的△A1B1C1,其中,点A, B,C的对称点分别为点A1,B1,C1;
(2)写出点C1的坐标__________;
(3)在平面直角坐标系中有一点P位于第四象限,其坐标表示为P(m,n),则点P关于直线l的对称点Q的坐标表示为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com