
分析 (1)由题目中所给和谐点对的定义可知P、Q即为关于原点对称的两个点,在反比例函数图象上找出两点即可;
(2)①由A、B为和谐点对可求得点B的坐标,则可得到关于m、n的方程组,可求得其值;②当M在x轴上方时,可先求得∠AMB为直角时对应的M点的坐标,当点M向上运动时满足∠AMB为锐角;当点M在x轴下方时,同理可求得b的取值范围.
解答 解:
(1)∵y=$\frac{1}{x}$,
∴可取[P(1,1),Q(-1,-1)];
(2)①∵A(2,4)且A和B为和谐点对,
∴B点坐标为(-2,-4),
将A和B两点坐标代入y=x2+mx+n,可得$\left\{{\begin{array}{l}{4+2m+n=4}\\{4-2m+n=-4}\end{array}}\right.$,
∴$\left\{{\begin{array}{l}{m=2}\\{n=-4}\end{array}}\right.$;
②(ⅰ) M点在x轴上方时,
若∠AMB 为直角(M点在x轴上),则△ABC为直角三角形,
∵A(2,4)且A和B为和谐点对,
∴原点O在AB线段上且O为AB中点,
∴AB=2OA,
∵A(2,4),
∴OA=$2\sqrt{5}$,
∴AB=$4\sqrt{5}$,
在Rt△ABC中,
∵O为AB中点
∴MO=OA=$2\sqrt{5}$,
若∠AMB 为锐角,则$b>2\sqrt{5}$;
(ⅱ) M点在x轴下方时,同理可得,$b<-2\sqrt{5}$,
综上所述,b的取值范围为$b>2\sqrt{5}$或$b<-2\sqrt{5}$.
点评 本题为反比例函数的综合应用,涉及中心对称、待定系数法、直角三角形的性质、方程思想及分类讨论思想等知识.在(1)中理解题目中所给的和谐点对的实质是关于原点对称的两个点是解题的关键,在(2)①中利用和谐点对的定义求得点B的坐标是解题的关键,在(2)②中求得使∠AMB为直角时点M的坐标是解题的关键.本题考查知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
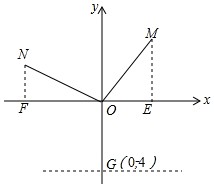 如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.
如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
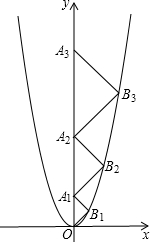 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 柑橘总质量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 损坏柑橘质量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 柑橘损坏的频率$\frac{m}{n}$ (结果保留小数点后三位) | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm.
如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com