

分析 (1)①根据反演点的定义求出OB′的长即可解决问题.
②解法一:过点P'作P'E⊥x轴于点E,如图3中,求出OF、PF即可解决问题.解法二:过点A作AH⊥PP'于点H,如图4中,求出OF、PF即可解决问题.
(2)①当点P是抛物线顶点(1,-4)时,作PE⊥x轴于E,过反演点P'作P′F⊥x轴于F.求出点P′的纵坐标即可.②当P点坐标为(4,5)时,求出反演点P'的纵坐标,即可解决问题.
解答 解:(1)如图2中,
∵OA•OA′=62,
∴OA′=6,
∴A′(6,0),
∵OB•OB′=62,
∴OB′=2,
∵∠AOB=135°,易知B′(-$\sqrt{2}$,$\sqrt{2}$).
故答案为A'(6,0),B′(-$\sqrt{2}$,$\sqrt{2}$).
②解法一:
过点P'作P'E⊥x轴于点E,如图3中,
∵S△OAP′=$\frac{1}{2}$•OA•P′E=6$\sqrt{3}$,
∴P′E=2$\sqrt{3}$,
∵点P'在正比例函数y=$\sqrt{3}$x位于第一象限内的图象上,
∴yP′=2$\sqrt{3}$,
∴xP'=2.
∴OP'=4,∠P'OE=60°.
∵点P关于⊙O的反演点是P'点,
∴OP'•OP=62.
∴OP=9.
过点P作PF⊥x轴于点F.
∴OF=$\frac{9}{2}$,PF=$\frac{9\sqrt{3}}{2}$,
∴点P的坐标为P($\frac{9}{2}$,$\frac{9\sqrt{3}}{2}$).
解法二:
过点A作AH⊥PP'于点H,如图4中,
∵点P'在正比例函数y=$\sqrt{3}x$位于第一象限内的图象上,
∴设点P的坐标为(t,$\sqrt{3}$t),其中t>0.
∴tan∠POA=$\frac{\sqrt{3}t}{t}$=$\sqrt{3}$,
∴∠POA=60°,
在Rt△OHA中,AH=OA•sin∠AOH=3$\sqrt{3}$,
∵S△OAP′=$\frac{1}{2}$•OP′•PAH=6$\sqrt{3}$,
∴OP'=4.
∵点P关于⊙O的反演点是P'点,
∴OP'•OP=62.
∴OP=9.
过点P作PF⊥x轴于点F.
在Rt△OFP中,t2+($\sqrt{3}$t)2=92,
解得t=$\frac{9}{2}$或-$\frac{9}{2}$(舍去),
∴点P的坐标为P($\frac{9}{2}$,$\frac{9\sqrt{3}}{2}$).
(2)如图5中,
①当点P是抛物线顶点(1,-4)时,作PE⊥x轴于E,过反演点P'作P′F⊥x轴于F.
∵OP=$\sqrt{17}$,r=$\frac{\sqrt{17}}{2}$,
∴OP′=$\frac{{r}^{2}}{OP}$=$\frac{\sqrt{17}}{4}$,
∵PE∥P′F,
∴$\frac{OP′}{OP}$=$\frac{P′F}{PE}$=$\frac{1}{4}$,
∴P′F=1,
∴n=-1,
②当P点坐标为(4,5)时,同法可得反演点P'的纵坐标n=$\frac{5}{4}$,
综上所述,-1≤n≤$\frac{5}{4}$.
点评 本题考查二次函数综合题、圆、勾股定理,平行线分线段成比例定理,解直角三角形等知识,解题的关键是理解题意,学会添加常用辅助线,属于中考创新题目.


科目:初中数学 来源: 题型:解答题
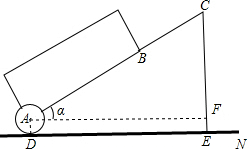 拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).
拉杆箱是人们出行的必需品,采用拉杆箱可以让我们的出行更轻松,如图,已知某种拉杆箱箱体长AB=50cm,拉杆最大伸长距离BC=40cm,点A到地面的距离AD=8cm,拉杆箱与水平面的夹角α的度数为35°.(提示:sin35°≈0.57,cos35°≈0.82).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 信件质量p(克) | 0<p≤20 | 20<p≤40 | 40<x≤60 |
| 邮资q(元) | 1.20 | 2.40 | 3.60 |
| A. | ①④ | B. | ①③ | C. | ③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com