

分析 (1)由B的人数和所占百分数求出共抽取的人数;再求出E和A的人数,由中位数的定义求出中位数,再将条形统计图补充完整即可;
(2)求出所抽取的20名同学的平均睡眠时间,即可得出结果.
解答 解: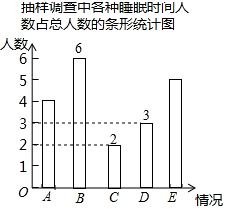 (1)共抽取的同学人数=6÷30%=20(人),
(1)共抽取的同学人数=6÷30%=20(人),
睡眠时间7小时左右的人数=20×$\frac{90°}{360°}$=5(人),睡眠时间8小时左右的人数=20-6-2-3-5=4(人),
按照睡眠时间从小到大排列,各组人数分别为2,3,6,5,4,睡眠时间分别为4,5,6,7,8,共有20个数据,
第10个和第11个数据都是6小时,它们的平均数也是6小时,
∴同学们的睡眠时间的中位数是6小时左右;
故答案为:20,6;
将条形统计图补充完整如图所示:
(2)∵平均数为$\frac{1}{20}$(4×8+6×6+2×4+3×5+5×7)=6.3(小时),
∴估计年级每个学生的平均睡眠时间约6.3小时.
点评 本题考查了条形统计呼和扇形统计图以及中位数和平均数的知识,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 如图,△ABC是等腰三角形,∠BAC=90°,D为BC延长线上一点,连续AD,以AD为边在AD右侧作正方形ADEF,连续FC、EC,若AC=$\sqrt{2}$,AD=$\sqrt{10}$.
如图,△ABC是等腰三角形,∠BAC=90°,D为BC延长线上一点,连续AD,以AD为边在AD右侧作正方形ADEF,连续FC、EC,若AC=$\sqrt{2}$,AD=$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
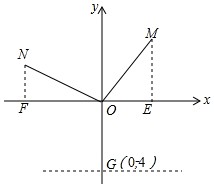 如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.
如图,在直角坐标系中,已知点M(2,3),连接OM,在第二象限作N,使ON⊥OM且ON=OM,y轴上有一点G(0,-4),过G作x轴的平行线l.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
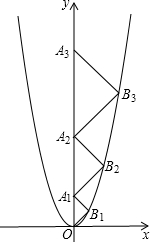 如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:
如图,在平面直角坐标系xOy中,点A1,A2,A3,…,An在y轴的正半轴上,点B1,B2,B3,…,Bn在二次函数y=x2位于第一象限的图象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm.
如图,等腰直角三角形ABC中,AB=4cm.点D是BC边上的动点,以AD为直角边作等腰直角三角形ADE.在点D从点B移动至点C的过程中,点E移动的路线长为4$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)
如图,已知四点A、B、C、D,请用尺规作图完成.(保留画图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com