
【题目】若如图,已知AD∥BC,按要求完成下列各小题(保留作图痕迹,不要求写作法).
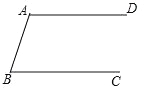
(1)用直尺和圆规作出∠BAD的平分线AP,交BC于点P.
(2)在(1)的基础上,若∠APB=55°,求∠B的度数.
(3)在(1)的基础上,E是AP的中点,连接BE并延长,交AD于点F,连接PF.求证:四边形ABPF是菱形.
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如下表是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?
阶梯 | 电量 | 电价 |
一档 | 0~180度 | 0.6元/度 |
二档 | 181~400度 | 二档电价 |
三档 | 401度及以上 | 三档电价 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
例如:①用配方法解题如下: ![]()
原式=![]() +6x+9+1=
+6x+9+1=![]()
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是0+1=1;所以当
的最小值是0+1=1;所以当![]() 时,原多项式的最小值是1.
时,原多项式的最小值是1.
请根据上面的解题思路,探求:
(1)若(x+1)2+(y-2)2=0,则x= ,y= ..
(2)若x2+y2+6x-4y+13=0,求x,y的值;
(3)求![]() 的最小值
的最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某钢铁企业为了适应市场竞争的需要,提高生产效率,决定将一部分钢铁生产一线员工调整去从事服务工作,该企业有钢铁生产一线员工1000人,平均每人可创造年产值30万元,根据规划,调整出去的一部分一线员工后,余下的生产一线员工平均每人全年创造年产值可增加30%,调整到服务性工作岗位人员平均每人全年可创造产值24万元,如果要保证员工岗位调整后,现在全年总产值至少增加20%,且钢铁产品的产值不能超过33150万元,怎样安排调整到服务行业的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面解答过程,并填空或填理由.
已知如下图,点E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H,∠A=∠D,∠1=∠2.
试说明:∠B=∠C.
解:∵∠1=∠2(已知)
∠2=∠3(___________)
∴∠3=∠1(等量代换)
∴AF∥DE(___________)
∴∠4=∠D(___________)
又∵∠A=∠D(已知)
∴∠A=∠4(等量代换)
∴AB∥CD(___________)
∴∠B=∠C(___________).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com