
【题目】已知在四边形ABCD中,∠A=∠C=90°.
(1)∠ABC+∠ADC= °;
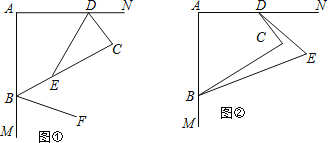
(2)如图①,若DE平分∠ADC,BF平分∠ABC的外角,请写出DE与BF的位置关系,并证明;
(3)如图②,若BE,DE分别四等分∠ABC、∠ADC的外角(即∠CDE=![]() ∠CDN,∠CBE=
∠CDN,∠CBE=![]() ∠CBM),试求∠E的度数.
∠CBM),试求∠E的度数.
【答案】(1)180°;(2)DE⊥BF;(3)450
【解析】
(1)根据四边形内角和等于360°列式计算即可得解;
(2)延长DE交BF于G,根据角平分线的定义可得∠CDE=![]() ∠ADC,∠CBF=
∠ADC,∠CBF=![]() ∠CBM,然后求出∠CDE=∠CBF,再利用三角形的内角和定理求出∠BGE=∠C=90°,最后根据垂直的定义证明即可;
∠CBM,然后求出∠CDE=∠CBF,再利用三角形的内角和定理求出∠BGE=∠C=90°,最后根据垂直的定义证明即可;
(3)先求出∠CDE+∠CBE,然后延长DC交BE于H,再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可.
(1)解:∵∠A=∠C=90°,
∴∠ABC+∠ADC=360°-90°×2=180°;
故答案为180°;
(2)解:延长DE交BF于G,
∵DE平分∠ADC,BF平分∠CBM,
∴∠CDE=![]() ∠ADC,∠CBF=
∠ADC,∠CBF=![]() ∠CBM,
∠CBM,
又∵∠CBM=180°-∠ABC=180°-(180°-∠ADC)=∠ADC,
∴∠CDE=∠CBF,
又∵∠BED=∠CDE+∠C=∠CBF+∠BGE,
∴∠BGE=∠C=90°,
∴DG⊥BF,
即DE⊥BF;
(3)解:由(1)得:∠CDN+∠CBM=180°,
∵BE、DE分别四等分∠ABC、∠ADC的外角,
∴∠CDE+∠CBE=![]() ×180°=45°,
×180°=45°,
延长DC交BE于H,
由三角形的外角性质得,∠BHD=∠CDE+∠E,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠E,
∴∠E=90°-45°=45°


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到![]() 世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若
世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,那么
,那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作:
的对数,记作:![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() );理由如下:设
);理由如下:设![]() M=m,
M=m,![]() ,则
,则![]() ,
,![]()
![]() ,由对数的定义得
,由对数的定义得![]() 又
又![]() +
+![]()
![]() .解决一下问题:
.解决一下问题:
(1)将指数式![]() 转化为对数式___________;
转化为对数式___________;
(2)证明![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() );
);
(3)拓展运用:计算![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
查看答案和解析>>
科目:初中数学 来源: 题型:
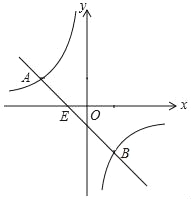
【题目】如图,已知A(﹣4,n),B(4﹣n,﹣4)是直线y=kx+b和双曲线y=![]() 的两个交点.
的两个交点.
(1)求两个函数的表达式;
(2)观察图象,直接写出不等式kx+b﹣![]() ≥0的解集.
≥0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc>0;②b<a+c;③4a﹣2b+c>0;④2c<3b;⑤当m≤x≤m+1时,函数的最大值为a+b+c,则0≤m≤1;
其中正确的结论有( )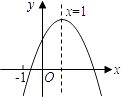
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com