
����Ŀ��A��B��C����������һ��ֱ����.�ף�������ͬʱ�ֱ���A,B������ֱ�����ٲ��е�C�أ�����C�ػ���m����.�����˳���x(����)ʱ������B�صľ���Ϊy(��)��y��x�ĺ���ͼ����ͼ��ʾ.

��1��A����C�صľ���Ϊ ����m= ��
��2����֪�ҵIJ����ٶ���40��/���ӣ����Ҳ���ʱ��B�صľ���Ϊy(��)��ֱ��д��y��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ������ͼ�л����˺�����ͼ��
��3���ҳ��������Ӻ�������;��������
���𰸡���1��1200,20����2��y1=40x(0��x��24����ͼ�����������3���ҳ���12���Ӻ�����������
�������������������1������ͼ��������![]() ֮��ľ��룬�ٶ�=·����ʱ��Ϳ���������ٶȣ�����ʱ��=·�����ٶȿ������
֮��ľ��룬�ٶ�=·����ʱ��Ϳ���������ٶȣ�����ʱ��=·�����ٶȿ������![]() ��ֵ.
��ֵ.
��2�����ã�1���Ľ���������ߵ�![]() �ص�ʱ�䣬�ô���ϵ�����Ϳ�������Ľ���ʽ���Ӷ����Ի�������ͼ�Σ�
�ص�ʱ�䣬�ô���ϵ�����Ϳ�������Ľ���ʽ���Ӷ����Ի�������ͼ�Σ�
��3����ͼ1�����![]() �Ľ���ʽ����������������Ϳ��Եó����ۣ�
�Ľ���ʽ����������������Ϳ��Եó����ۣ�
���������(1)��ͼ��ã�AC�ľ���Ϊ��240+960=1200�ף�
���ٶ�Ϊ��240��4=60��/�֣�
960 ��60=16�֣�
![]()
�ʴ�Ϊ��1200,20.
��2������ʽΪ![]()
��������ͼ��Ϊ

(3)��ͼ1���߶�![]() ����
����![]() �����㣬
�����㣬
��![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��ͼ���
��ͼ���![]() ��
��
��ã� ![]()
![]()
��![]() ��
��
��ã� ![]()
���ҳ���12���Ӻ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڿ�չ ��У�װ���������������ϲ�ɽ��ѧУ�����С�Ů���ֿ�ʽ���������֪�п�����ĵ���50Ԫ/����Ů������ĵ���70Ԫ/����
��1��ԭ�ƻ�ļ��3400Ԫ���������ֿ�ʽ�������60������ô�����ֿ�ʽ�����������ٸ���
��2���ھ����������ѧ�����Ļ����Ը�����ʵ�ʹ����4800Ԫ��������ٹ������ֿ�ʽ�������80������ôŮ��������������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�
һ��أ���������Ϊ�����ʱ��tan����+�£���tan�������£���ֵ����������Ĺ�ʽ��ã�tan�������£�=![]() ��
��
���磺tan15��=tan��45�㩁30�㣩=![]() =
= =
=![]()
= =
=![]() ��
��
�������ϲ��ϣ�����������⣺
��1����tan75���ֵ��
��2�������ķ�����ԭ���ı�����ʼ��������������䣬ϵ���ľ�����ķ�����ľ�������٣�����������1983�꣬������������ά���ķ�������Ϊ������߲�����ʵ��ʯ����ͼ1����С��������ѧ֪ʶ������������ĸ߶ȣ���ͼ2����֪С��վ������������A��5.7��C�����������������Ϊ75�㣬С�����۾������ľ���DCΪ1.72�ף������С������ķ���AB�ĸ߶ȣ�����ȷ��1�ף��ο�����![]() ��1.732��
��1.732�� ![]() ��1.414��
��1.414��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P������Ϊ(a��1��5��2a)������������������ľ�����ȣ����P������Ϊ(����)
A.(3��3)B.(3����3)C.(1����1)D.(1��1)��(3����3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������������Ϸ��С��ÿ�δ��������ó�8��������ͷŻ�ȥ3���������й���108����
��1����һ���ó���������ʣ���� ������
��2��С��Ҫȡ���ٴβ��ܰ���ȫ���ó�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������A�dz���������ʻ��B�ǣ���������ʻ�����У��ס��������뿪A�ǵľ���y��ǧ�ף���׳���ʻ��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ�
��A��B�������300ǧ�ף�
���ҳ��ȼ׳�������1Сʱ��ȴ�絽1Сʱ��
���ҳ�������2.5Сʱ�ϼ׳���
�ܵ��ס����������50ǧ��ʱ��t=![]() ��
��![]() ��
��
������ȷ�Ľ����У� ��

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
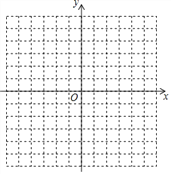
����Ŀ����1������ͼ��ʾ��ƽ��ֱ������ϵ�б�ʾ������㣺A��0��3����B��5��0����C��3��-5����D��-3��-5����E��3��5����
��2������CE����ֱ��CE��y����ʲôλ�ù�ϵ��
��3����D�ֱ�x��y��ľ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com