
分析 首先根据一元二次方程根的判别式可得b2-4×1×c=b2-4c>0,再根据二次函数的顶点坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$)可表示出抛物线y=x2+bx+c的顶点坐标,然后再判断所在象限即可.
解答 解:∵关于x的方程x2+bx+c=0(b<0)有两个不相等的实数根,
∴△>0,
∴b2-4×1×c=b2-4c>0,
抛物线y=x2+bx+c的顶点坐标为(-$\frac{b}{2}$,$\frac{4c-{b}^{2}}{4}$),
∵b<0,
∴-$\frac{b}{2}$>0,
∵b2-4c>0,
∴$\frac{4c-{b}^{2}}{4}$<0,
∴顶点一定在第四象限上.
故答案为:四.
点评 此题主要考查了抛物线与一元二次方程,关键是掌握一元二次方程根的判别式和二次函数的顶点坐标(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
 用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )
用“●”“■”“”分别表物体,如图所示,前两架天平保持平衡,若要使第三架天平也平衡,那么“?”处应放“■”的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
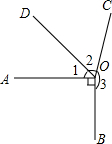 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
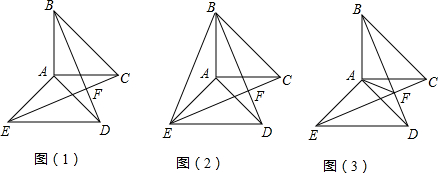
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com