
分析 (1)先去括号,再化成最简二次根式,最后合并同类二次根式;
(2)把被开方数相乘除,得出结果;
(3)先把第一个括号内的数交换加数的位置变为3$\sqrt{2}$+1,再利用平方差公式进行计算;
(4)利用完全平方公式展开.
解答 解:(1)($\sqrt{24}$+$\sqrt{8}$)-($\sqrt{2}$+$\sqrt{6}$),
=2$\sqrt{6}$+2$\sqrt{2}$-$\sqrt{2}$-$\sqrt{6}$,
=(2-1)$\sqrt{6}$+(2-1)$\sqrt{2}$,
=$\sqrt{6}$+$\sqrt{2}$;
(2)$\sqrt{\frac{5}{2}}$÷$\sqrt{\frac{3}{2}}$×$\sqrt{3}$,
=$\sqrt{\frac{5}{2}×\frac{2}{3}×3}$,
=$\sqrt{5}$;
(3)(1+3$\sqrt{2}$)(3$\sqrt{2}$-1),
=(3$\sqrt{2}$+1)(3$\sqrt{2}$-1),
=(3$\sqrt{2}$)2-1,
=18-1,
=17;
(4)($\sqrt{2}$+2$\sqrt{3}$)2,
=$(\sqrt{2})^{2}$+2×$2\sqrt{3}$×$\sqrt{2}$+$(2\sqrt{3})^{2}$,
=2+4$\sqrt{6}$+12,
=14+4$\sqrt{6}$.
点评 本题是二次根式的混合运算,与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的;要注意二次根式的运算结果要化为最简二次根式.


科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
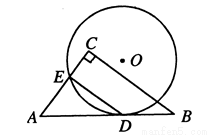
如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于点E,且DE∥BC.已知AE=2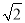 ,AC=3
,AC=3 ,BC=6,则⊙O的半径是__________________.
,BC=6,则⊙O的半径是__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 胜3局与负4局 | B. | 收入3000元与支出2000元 | ||
| C. | 气温升高4℃与气温升高10℃ | D. | 转盘逆时针转3圈与顺时针转5圈 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AC=8,AB=10,∠BAC=60°,⊙O与AB,AC都相切,与AB的切点为E.
如图,在△ABC中,AC=8,AB=10,∠BAC=60°,⊙O与AB,AC都相切,与AB的切点为E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=2,y=3 | B. | 2x=3y | C. | $\frac{x+y}{y}=\frac{5}{3}$ | D. | $\frac{x+2}{y+3}=\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 25(1+x)2=64 | B. | 25(1-x)2=64 | C. | 64(1+x)2=25 | D. | 64(1-x)2=25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com