练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

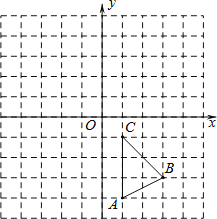
    【题目】如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，﹣4）、B（3，﹣3）、C（1，﹣1）（每个小方格都是边长为一个单位长度的正方形）．

    （1）请画出△ABC关于原点对称的△A1B1C1，并写出A1，B1，C1的坐标；

    （2）请画出△ABC绕点B逆时针旋转90°后的△A2B2C2．

    【答案】（1）见解析，点A1，B1，C1的坐标分别为（﹣1，4），（﹣3，3），（﹣1，1）；（2）见解析．

    【解析】

    （1）根据中心对称图形的概念即可作出图形，求出对应点坐标；

    （2）根据旋转作图的方法即可．

    （1）如图，△A1B1C1为所作，点A1，B1，C1的坐标分别为（﹣1，4），（﹣3，3），（﹣1，1）；

    （2）如图，△A2B2C2为所作．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

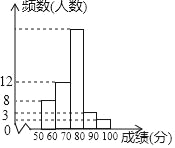
    【题目】（7分）某中学1000名学生参加了”环保知识竞赛“，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）．请解答下列问题：

    成绩分组

    频数

    频率

    50≤x＜60

    8

    0.16

    60≤x＜70

    12

    a

    70≤x＜80

    ■

    0.5

    80≤x＜90

    3

    0.06

    90≤x≤100

    b

    c

    合计

    ■

    1

    （1）写出a，b，c的值；

    （2）请估计这1000名学生中有多少人的竞赛成绩不低于70分；

    （3）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取两名同学参加环保知识宣传活动，求所抽取的2名同学来自同一组的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为倡导“低碳生活”，常选择以自行车作为代步工具．如图1所示是一辆自行车的实物图，车架档AC与CD的长分别为45cm，60cm，且它们互相垂直，座杆CE的长为20cm，车轮半径28cm，点A，C，E在同一条直线上，且∠CAB=75°，如图2

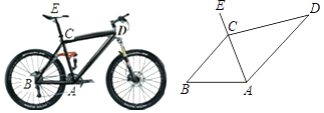
    图1 图2

    （1）求车座点E到地面的距离；（结果精确到1cm）

    （2）求车把点D到车架档直线AB的距离．（结果精确到1cm）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了了解班级学生数学课前预习的具体情况，郑老师对本班部分学生进行了为期一个月的跟踪调查，他将调查结果分为四类：A：很好；B：较好；C：一般；D：不达标，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

    （1）C类女生有　 　名，D类男生有　 　名，将上面条形统计图补充完整；

    （2）扇形统计图中“课前预习不达标”对应的圆心角度数是　 　；

    （3）为了共同进步，郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习，请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率，

    查看答案和解析>>

    科目：初中数学 来源： 题型：

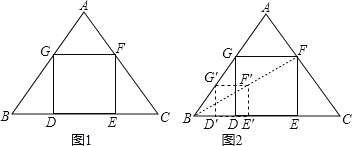
    【题目】如图，△ABC是一块等边三角形的废铁片，其中AB=AC=10，BC=12．利用其剪裁一个正方形DEFG，使正方形的一条边DE落在BC上，顶点F． G分别落在AC、AB上．

    （1）小聪想：要画出正方形DEFG，只要能计算出正方形的边长就能求出BD和CE的长，从而确定D点和E点，再画正方形DEFG就容易了．请你帮小聪求出正方形的边长．

    （2）小明想：不求正方形的边长也能画出正方形．具体作法是：

    ①在AB边上任取一点G′，如图2作正方形G′D′E′F′；

    ②连接BF′并延长交AC于点F；

    ③过点F作FE∥F′E′交BC于点E，FG∥F′G′交AB于点G，GD∥G′D′交BC于点D，则四边形DEFG即为所求的正方形．你认为小明的作法正确吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，点P是等边△ABC内一点，已知PA＝3，PB＝4，PC＝5，求∠APB的度数．

    要直接求∠A的度数显然很因难，注意到条件中的三边长恰好是一组勾股数，因此考虑借助旋转把这三边集中到一个三角形内．

    解：如图2，作∠PAD＝60°使AD＝AP，连接PD，CD，则△PAD是等边三角形．

    ∴　 　＝AD＝AP＝3，∠ADP＝∠PAD＝60°

    ∵△ABC是等边三角形

    ∴AC＝AB，∠BAC＝60°∴∠BAP＝　 　

    ∴△ABP≌△ACD

    ∴BP＝CD＝4，　 　＝∠ADC

    ∵在△PCD中，PD＝3，PC＝5，CD＝4，PD2+CD2＝PC2

    ∴∠PDC＝　 　°

    ∴∠APB＝∠ADC＝∠ADP+∠PDC＝60°+90°＝150°

    （2）如图3，在△ABC中，AB＝BC，∠ABC＝90°，点P是△ABC内一点，PA＝1，PB＝2，PC＝3，求∠APB的度数．

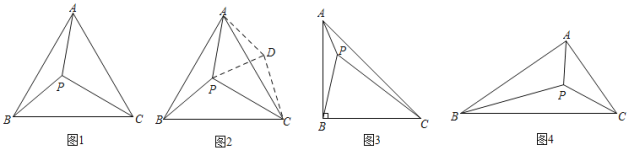
    （3）拓展应用．如图4，△ABC中，∠ABC＝30°，AB＝4，BC＝5，P是△ABC内部的任意一点，连接PA，PB，PC，则PA+PB+PC的最小值为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

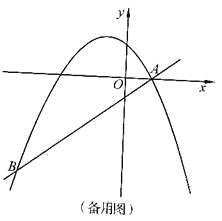
    【题目】如图，在平面直角坐标系中，直线与抛物线交于A、B两点，点A在x轴上，点B的横坐标为－8.

    （1）求该抛物线的解析式；

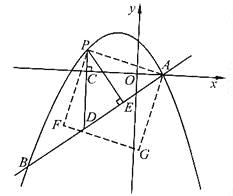
    （2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.

    ①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；

    ②连接PA，以PA为边作图示一侧的正方形APFG.随着点P的运动，正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点 A 和点 C 分别在x 轴和 y 轴的正半轴上，OA=6，OC=4，以 OA，OC 为邻边作矩形 OABC， 动点 M，N 以每秒 1 个单位长度的速度分别从点 A、C 同时出发，其中点 M 沿 AO 向终点 O 运动，点 N沿 CB 向终点 B 运动，当两个动点运动了 t 秒时，过点 N 作NP⊥BC，交 OB 于点 P，连接 MP．

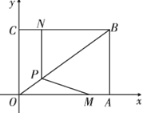
    （1）直接写出点 B 的坐标为 ，直线 OB 的函数表达式为 ;

    （2）记△OMP 的面积为 S，求 S 与 t 的函数关系式；并求 t 为何值时，S有最大值，并求出最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠ACB＝90°，点D、E分别是AB、BC的中点，过点C作CF∥AB，与DE的延长线并交于点F，连接BF．

    （1）试判断四边形CDBF的形状，并说明理由；

    （2）若CD＝5，sin∠CAB＝，过点C作CH⊥BF，垂足为H点，试求CH的长．

    查看答案和解析>>

    同步练习册答案