
【题目】已知抛物线![]() ,直线
,直线![]() 的对称轴与
的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 与
与![]() 的顶点
的顶点![]() 的距离是4.
的距离是4.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() 与
与![]() 都经过
都经过![]() 轴上的同一点,求
轴上的同一点,求![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)
;(2)![]() 或者
或者![]() .
.
【解析】试题分析:(1)利用二次函数的对称轴公式求出m,再利用两点间的距离公式求出n;
(2)根据一次函数的性质求出k大于0,注意分类讨论解决问题,用待定系数法求一次函数的表达式.
试题解析:(1)![]() 的对称轴与
的对称轴与![]() 的交点为
的交点为![]() ,
,
![]() 的对称轴为
的对称轴为![]() ,
, ![]() ,
,
![]() ,
,
![]() 顶点坐标为
顶点坐标为![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)①当![]() 时,
时, ![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() ,
,
ⅰ.当![]() 经过点
经过点![]() 时,则有
时,则有![]() , 解得
, 解得![]() ,
,
∴![]() (不符,舍去);
(不符,舍去);
ⅱ.当![]() 经过点
经过点![]() 时,则有
时,则有![]() ,
, ![]() ,
,
![]() ;
;
②当![]() 时,令
时,令![]() 则
则![]() ,则
,则![]() ,
,
![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
ⅰ.当![]() 经过点
经过点![]() 时,则有
时,则有![]() ,
, 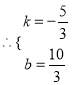 ,
,
∴![]() (不符,舍去);
(不符,舍去);
ⅱ.当![]() 经过点
经过点![]() 时, 则有
时, 则有![]() ,
, 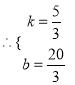 ,
,
![]() ,
,
综上述, ![]() 或者
或者![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ∥
∥![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

解:因为![]() ∥
∥![]() (已知),
(已知),
所以![]() (__________________________).
(__________________________).
因为![]() (____________________________),
(____________________________),
所以![]() (等量代换).
(等量代换).
(余下说理过程请写在下方)
查看答案和解析>>
科目:初中数学 来源: 题型:
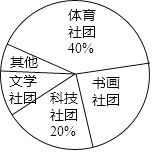
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的面积为1.分别倍长(延长一倍)
的面积为1.分别倍长(延长一倍)![]() ,BC,CA得到
,BC,CA得到![]() .再分别倍长A1B1,B1C1,C1A1得到
.再分别倍长A1B1,B1C1,C1A1得到![]() .…… 按此规律,倍长2018次后得到的
.…… 按此规律,倍长2018次后得到的![]() 的面积为( )
的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【新知理解】
如图①,若点![]() 、
、![]() 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点![]() ,使
,使![]() 的值最小.
的值最小.
作法:作点![]() 关于直线l的对称点
关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点
交直线l于点![]() ,则点
,则点![]() 即为所求.
即为所求.
【解决问题】
如图②,![]() 是边长为6cm的等边三角形
是边长为6cm的等边三角形![]() 的中线,点
的中线,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,则
上,则![]() 的最小值为 cm;
的最小值为 cm;
【拓展研究】
如图③,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)

查看答案和解析>>
科目:初中数学 来源: 题型:
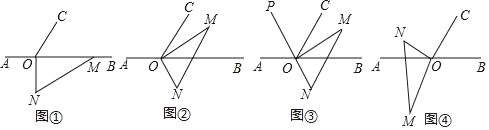
【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角板OMN摆放成如图②所示的位置,使一边OM在∠BOC的内部,当OM平分∠BOC时,∠BON= ;(直接写出结果)
(2)在(1)的条件下,作线段NO的延长线OP(如图③所示),试说明射线OP是∠AOC的平分线;
(3)将图①中的三角板OMN摆放成如图④所示的位置,请探究∠NOC与∠AOM之间的数量关系.(直接写出结果,不须说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com