
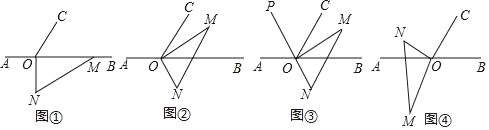
【题目】如图①,点O为直线AB上一点,过点O作射线OC,使∠AOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图①中的三角板OMN摆放成如图②所示的位置,使一边OM在∠BOC的内部,当OM平分∠BOC时,∠BON= ;(直接写出结果)
(2)在(1)的条件下,作线段NO的延长线OP(如图③所示),试说明射线OP是∠AOC的平分线;
(3)将图①中的三角板OMN摆放成如图④所示的位置,请探究∠NOC与∠AOM之间的数量关系.(直接写出结果,不须说明理由)
【答案】(1)60°;(2)射线OP是∠AOC的平分线;(3)30°.
【解析】整体分析:
(1)根据角平分线的定义与角的和差关系计算;(2)计算出∠AOP的度数,再根据角平分线的定义判断;(3)根据∠AOC,∠AON,∠NOC,∠MON,∠AOM的和差关系即可得到∠NOC与∠AOM之间的数量关系.
解:(1)如图②,∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
又∵OM平分∠BOC,
∴∠BOM=30°,
又∵∠NOM=90°,
∴∠BOM=90°﹣30°=60°,
故答案为60°;
(2)如图③,∵∠AOP=∠BOM=60°,∠AOC=120°,
∴∠AOP=![]() ∠AOC,
∠AOC,
∴射线OP是∠AOC的平分线;
(3)如图④,∵∠AOC=120°,
∴∠AON=120°﹣∠NOC,
∵∠MON=90°,
∴∠AON=90°﹣∠AOM,
∴120°﹣∠NOC=90°﹣∠AOM,
即∠NOC﹣∠AOM=30°.


科目:初中数学 来源: 题型:
【题目】为了锻炼学生身体素质,训练定向越野技能,某校在一公园内举行定向越野挑战赛.路线图如图![]() 所示,点
所示,点![]() 为矩形
为矩形![]() 边
边![]() 的中点,在矩形
的中点,在矩形![]() 的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员
的四个顶点处都有定位仪,可监测运动员的越野进程,其中一位运动员![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路线匀速行进,到达点
的路线匀速行进,到达点![]() .设运动员
.设运动员![]() 的运动时间为
的运动时间为![]() ,到监测点的距离为
,到监测点的距离为![]() .现有
.现有![]() 与
与![]() 的函数关系的图象大致如图
的函数关系的图象大致如图![]() 所示,则这一信息的来源是( ).
所示,则这一信息的来源是( ).


A. 监测点![]() B. 监测点
B. 监测点![]() C. 监测点
C. 监测点![]() D. 监测点
D. 监测点![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
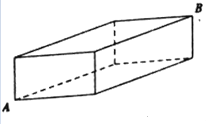
【题目】如图,长方体的长、宽、高分别为6cm,4cm,2cm,现有一只蚂蚁点A出发,沿长方体表面达到B处,则所走的最短路径是 __________ cm。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一条抛物线经过A(0,3),B(4,6)两点,对称轴是x=![]() .
.
(1)求这条抛物线的关系式.
(2)证明:这条抛物线与x轴的两个交点中,必存在点C,使得对x轴上任意点D都有AC+BC≤AD+BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
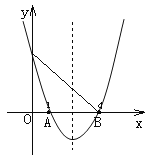
【题目】已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:
(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______;![]() =_________,
=_________,![]() =________.
=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
查看答案和解析>>
科目:初中数学 来源: 题型:
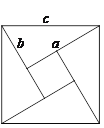
【题目】如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为![]() ,较短的直角边为
,较短的直角边为![]() ,斜边长为
,斜边长为![]() ,试利用图①验证勾股定理;
,试利用图①验证勾股定理;
(2)如图②,将这四个全等的直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(实线)的周长为![]() ,
, ![]() ,求该飞镖状图案的面积;
,求该飞镖状图案的面积;
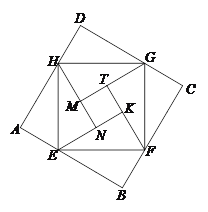
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的面积分别为
的面积分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则
,则![]() =________.
=________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com