
分析 利用二次根式的乘法、除法法则即可化简.
①分别分母有理化即可.
②根据分母有理化法则以及平方差公式化简即可.
解答 解:$\sqrt{8}$=$\sqrt{2×4}$=$\sqrt{4}$×$\sqrt{2}$=2$\sqrt{2}$,$\sqrt{\frac{5}{2}}$=$\sqrt{\frac{10}{4}}$=$\frac{\sqrt{10}}{\sqrt{4}}$=$\frac{\sqrt{10}}{2}$,
故答案为2$\sqrt{2}$,$\frac{\sqrt{10}}{2}$.
①$\frac{6}{\sqrt{3}}$=$\frac{6\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{6\sqrt{3}}{3}$=2$\sqrt{3}$,$\frac{2}{\sqrt{2}-1}$=$\frac{2(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}$=2$\sqrt{2}$+2.
故答案为2$\sqrt{3}$,2$\sqrt{2}$+2.
②原式=$\frac{(\sqrt{3}+1)^{2}}{(\sqrt{3}-1)(\sqrt{3}+1)}$-[(3$\sqrt{2}$)2-(2$\sqrt{3}$)2]=$\frac{4+2\sqrt{3}}{2}$-6=2+$\sqrt{3}$-6=$\sqrt{3}$-4.
点评 本题考查二次根式的化简,解题的关键是学会分母有理化、利用平方差公式化简,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
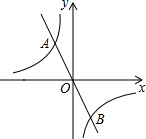 如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点
如图示,双曲线y=$\frac{{k}_{1}}{x}$与直线y=k2x交于A(-1,m)、B(n,-2)两点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
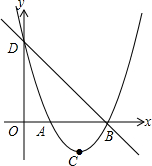 如图所示,已知二次函数y=x2-4x+m,它的图象与x轴交于A,B两点(A在B的左侧),与y轴交于点D,且满足OB=OD,顶点为C
如图所示,已知二次函数y=x2-4x+m,它的图象与x轴交于A,B两点(A在B的左侧),与y轴交于点D,且满足OB=OD,顶点为C查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
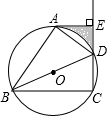 如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.
如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com