

���� ��1������ϲ����������18�ˣ����ݶ�Ӧ��Բ�ĽǼ��������ռ�ı���������18������ռ�ı������������������������÷dz�ϲ�����������Ӷ���ȫ����ͳ��ͼ��
��2������������540���Զ�Ӧ�ı���������⣮
��� �⣺��1�����ε���İ��꼶����ѧ������18��$\frac{120��}{360��}$=54���ˣ���
���dz�ϲ����������Ϊ��54-18-6=30���ˣ���
��ȫ����ͳ��ͼ��ͼ��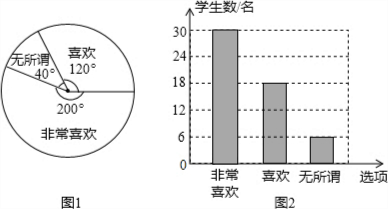
��2��$\frac{30+18}{54}$��540=480���ˣ���
�𣺹��Ƹ�У���꼶��480��ѧ��֧�֡��������ѧϰ����ʽ��
�ʴ�Ϊ����1��54��
���� ���⿼���������ͳ��ͼ������ͳ��ͼ���ۺ����ã�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
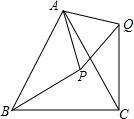 ��ͼ���ȱߡ�ABC�У���P�ڡ�ABC�ڣ���Q�ڡ�ABC�⣬�ҡ�ABP=��ACQ��BP=CQ��
��ͼ���ȱߡ�ABC�У���P�ڡ�ABC�ڣ���Q�ڡ�ABC�⣬�ҡ�ABP=��ACQ��BP=CQ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
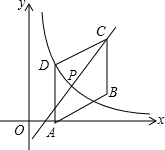 ��ͼ���ı���ABCD��ƽ���ı��Σ���A��1��0����B��3��1����C��3��3��������������y=$\frac{m}{x}$��x��0����ͼ����D����1��2��
��ͼ���ı���ABCD��ƽ���ı��Σ���A��1��0����B��3��1����C��3��3��������������y=$\frac{m}{x}$��x��0����ͼ����D����1��2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����D��$\widehat{BC}$���е㣬DE��AB��E����CB�ڵ�F������D��BC��ƽ����DM������AC���ӳ���DM�ཻ�ڵ�G��
��ͼ��AB�ǡ�O��ֱ����D��$\widehat{BC}$���е㣬DE��AB��E����CB�ڵ�F������D��BC��ƽ����DM������AC���ӳ���DM�ཻ�ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
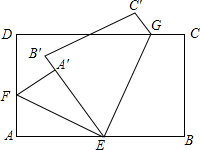 ��ͼ������������Ƭ�۵����ۺ�ΪEF��EG����A����A������B����B�䴦����EA���EB���غϣ�
��ͼ������������Ƭ�۵����ۺ�ΪEF��EG����A����A������B����B�䴦����EA���EB���غϣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com