
【题目】如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2 ![]() ,DE=2,则四边形OCED的面积( )
,DE=2,则四边形OCED的面积( ) 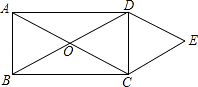
A.2 ![]()
B.4
C.4 ![]()
D.8
【答案】A
【解析】解:连接OE,与DC交于点F, 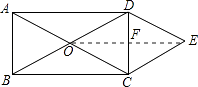
∵四边形ABCD为矩形,
∴OA=OC,OB=OD,且AC=BD,即OA=OB=OC=OD,
∵OD∥CE,OC∥DE,
∴四边形ODEC为平行四边形,
∵OD=OC,
∴四边形ODEC为菱形,
∴DF=CF,OF=EF,DC⊥OE,
∵DE∥OA,且DE=OA,
∴四边形ADEO为平行四边形,
∵AD=2 ![]() ,DE=2,
,DE=2,
∴OE=2 ![]() ,即OF=EF=
,即OF=EF= ![]() ,
,
在Rt△DEF中,根据勾股定理得:DF= ![]() =1,即DC=2,
=1,即DC=2,
则S菱形ODEC= ![]() OEDC=
OEDC= ![]() ×2
×2 ![]() ×2=2
×2=2 ![]() .
.
故选A
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】温度通常有两种表示方法:华氏度(单位:℉)与摄氏度(单位:℃),已知华氏度数y与摄氏度数x之间是一次函数关系,如表列出了部分华氏度与摄氏度之间的对应关系:
摄氏度数x(℃) | … | 0 | … | 35 | … | 100 | … |
华氏度数y(℉) | … | 32 | … | 95 | … | 212 | … |
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是﹣5℃,求与之对应的华氏度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程kx2+(k+2)x+ ![]() =0有两个不相等的实数根;
=0有两个不相等的实数根;
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以直角三角形a、b、c为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四种情况的面积关系满足S1+S2=S3图形个数有( ) 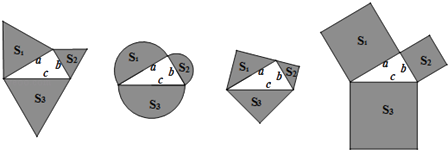
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某创业团队有研发、管理和操作三个小组,各组的日工资和人数如下表:
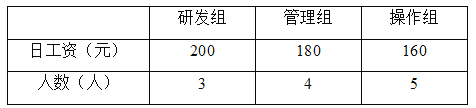
现从管理组分别抽调1人到研发组和操作组,调整后与调整前相比,下列说法中正确的有( )
①平均日工资增大 ②日工资的方差减小
③日工资的中位数不变 ④日工资的众数不变
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( ) 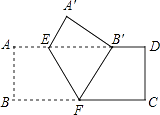
A.12
B.24
C.12 ![]()
D.16 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com