练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某地居民生活用电基本价格为每度电0.4元，若每月用电量不超过度时，按基本价格收费；若超过度，超出部分按基本价格的150%收费.

    （1）某户8月份用电84度，共交电费38.4元，求的值。

    （2）如果该户9月份的电费平均为每度0.5元，那么该用户9月份用电多少度？应交电费多少元？

    【答案】该用户9月份用电120度，应交电费60元

    【解析】

    （1）根据题意可知8月份用电84度，电费的计算方法为：0.40x+（84-x）×0.40×150%由此即可列方程，解方程即可解决；（2）设该户9月份用电度，电费的计算两种方法为：①0.40x+（y-x）×0.40×150%，②由此即可列方程，解方程求解即可．

    （1）

    （2）设该户9月份用电度，依题意得：

    （元）

    答：该用户9月份用电120度，应交电费60元。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c的图象经过点A（m，0），B（0，n），如图所示．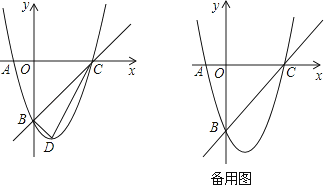
    （1）求这个抛物线的解析式；
    （2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，试求出点C，D的坐标，并判断△BCD的形状；
    （3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为 个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某自行车厂一周计划生产1400辆自行车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入表是某周的生产情况超产为正、减产为负：

    星期

    一

    二

    三

    四

    五

    六

    日

    增减

    根据记录可知前三天共生产多少辆；

    产量最多的一天比产量最少的一天多生产多少辆；

    该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班将买一些乒乓球和乒乓球拍．了解信息如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍．乒乓球拍每副定价30元，乒乓球每盒定价5元；经洽谈：甲店每买一副球拍赠一盒乒乓球；乙店全部按定价的9折优惠．该班需球拍5副，乒乓球若干盒(不小于5盒)．问：

    (1)当购买乒乓球x盒时，两种优惠办法各应付款多少元？(用含x的代数式表示)

    (2)如果要购买15盒乒乓球时，请你去办这件事，你打算去哪家商店购买？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某地生产一种绿色蔬菜，若在市场上直接销售，每吨利润为1 000元；经粗加工后销售，每吨利润可达4 500元；经精加工后销售，每吨利润涨至7 500元．

    当地一家蔬菜公司收获这种蔬菜140吨，该公司加工厂的生产能力是：如果对蔬菜进行粗加工，每天可加工16吨；如果进行精加工，每天可加工6吨，但两种加工方式不能同时进行，受季节等条件限制，公司必须在15天内将这批蔬菜全部销售或加工完毕，为此公司制订了三种方案：

    方案一：将蔬菜全部进行粗加工；

    方案二：尽可能多的对蔬菜进行精加工，没有来得及进行加工的蔬菜，在市场上直接销售；

    方案三：将部分蔬菜进行精加工，其余蔬菜进行粗加工，并恰好15天完成．

    你认为选择哪种方案获利最多？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“保护好环境，拒绝冒黑烟”．某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
    （1）求购买A型和B型公交车每辆各需多少万元？
    （2）预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥FC，D是AB上一点，DF交AC于点E，DE=FE，分别延长FD和CB交于点G．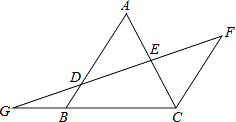
    （1）求证：△ADE≌△CFE；
    （2）若GB=2，BC=4，BD=1，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．

    （1）如图1，求证：△AFB≌△ADC；

    （2）请判断图1中四边形BCEF的形状，并说明理由；

    （3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线．
    （1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线．
    （2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数．
    （3）如图2，△ABC中，AC=2，BC= ，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长．

    查看答案和解析>>

    同步练习册答案