
ΓΨΧβΡΩΓΩ“―÷ΣΘ§mΘ§n «“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2+4x+3=0ΒΡΝΫΗω Β ΐΗυΘ§«“|m|ΘΦ|n|Θ§≈ΉΈοœΏy=x2+bx+cΒΡΆΦœσΨ≠ΙΐΒψAΘ®mΘ§0Θ©Θ§BΘ®0Θ§nΘ©Θ§»γΆΦΥυ ΨΘ°
Θ®1Θ©«σ’βΗω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©…ηΘ®1Θ©÷–ΒΡ≈ΉΈοœΏ”κx÷αΒΡΝμ“ΜΗωΫΜΒψΈΣ≈ΉΈοœΏΒΡΕΞΒψΈΣDΘ§ ‘«σ≥ωΒψCΘ§DΒΡΉχ±ξΘ§≤Δ≈–ΕœΓςBCDΒΡ–ΈΉ¥ΘΜ
Θ®3Θ©ΒψP «÷±œΏBC…œΒΡ“ΜΗωΕ·ΒψΘ®ΒψP≤Μ”κΒψBΚΆΒψC÷ΊΚœΘ©Θ§ΙΐΒψPΉςx÷αΒΡ¥ΙœΏΘ§ΫΜ≈ΉΈοœΏ”ΎΒψMΘ§ΒψQ‘Ύ÷±œΏBC…œΘ§ΨύάκΒψPΈΣ ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§…ηΒψPΒΡΚαΉχ±ξΈΣtΘ§ΓςPMQΒΡΟφΜΐΈΣSΘ§«σ≥ωS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ°
ΗωΒΞΈΜ≥ΛΕ»Θ§…ηΒψPΒΡΚαΉχ±ξΈΣtΘ§ΓςPMQΒΡΟφΜΐΈΣSΘ§«σ≥ωS”κt÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©
ΫβΘΚΓΏx2+4x+3=0Θ§
Γύx1=©¹1Θ§x2=©¹3Θ§
ΓΏmΘ§n «“Μ‘ΣΕΰ¥ΈΖΫ≥Χx2+4x+3=0ΒΡΝΫΗω Β ΐΗυΘ§«“|m|ΘΦ|n|Θ§
Γύm=©¹1Θ§n=©¹3Θ§
ΓΏ≈ΉΈοœΏy=x2+bx+cΒΡΆΦœσΨ≠ΙΐΒψAΘ®mΘ§0Θ©Θ§BΘ®0Θ§nΘ©Θ§
Γύ ![]() Θ§
Θ§
Γύ ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣy=x2©¹2x©¹3Θ§
Θ®2Θ©
ΫβΘΚΝνy=0Θ§‘ρx2©¹2x©¹3=0Θ§
Γύx1=©¹1Θ§x2=3Θ§
ΓύCΘ®3Θ§0Θ©Θ§
ΓΏy=x2©¹2x©¹3=Θ®x©¹1Θ©2©¹4Θ§
ΓύΕΞΒψΉχ±ξDΘ®1Θ§©¹4Θ©Θ§
ΙΐΒψDΉςDEΓΆy÷αΘ§
ΓΏOB=OC=3Θ§
ΓύBE=DE=1Θ§
ΓύΓςBOCΚΆΓςBEDΕΦ «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœOBC=ΓœDBE=45ΓψΘ§
ΓύΓœCBD=90ΓψΘ§
ΓύΓςBCD «÷±Ϋ«»ΐΫ«–Έ
Θ®3Θ©
ΫβΘΚ»γΆΦΘ§
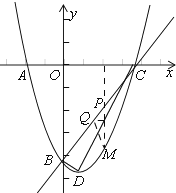
ΓΏBΘ®0Θ§©¹3Θ©Θ§CΘ®3Θ§0Θ©Θ§
Γύ÷±œΏBCΫβΈω ΫΈΣy=x©¹3Θ§
ΓΏΒψPΒΡΚαΉχ±ξΈΣtΘ§PMΓΆx÷αΘ§
ΓύΒψMΒΡΚαΉχ±ξΈΣtΘ§
ΓΏΒψP‘Ύ÷±œΏBC…œΘ§ΒψM‘Ύ≈ΉΈοœΏ…œΘ§
ΓύPΘ®tΘ§t©¹3Θ©Θ§MΘ®tΘ§t2©¹2t©¹3Θ©Θ§
ΙΐΒψQΉςQFΓΆPMΘ§
ΓύΓςPQF «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓΏPQ= ![]() Θ§
Θ§
ΓύQF=1Θ§
Β±ΒψP‘ΎΒψM…œΖΫ ±Θ§Φ¥0ΘΦtΘΦ3 ±Θ§
PM=t©¹3©¹Θ®t2©¹2t©¹3Θ©=©¹t2+3tΘ§
ΓύS= ![]() PMΓΝQF=
PMΓΝQF= ![]() Θ®©¹t2©¹3tΘ©=©¹
Θ®©¹t2©¹3tΘ©=©¹ ![]() t2+
t2+ ![]() tȧ
tȧ
»γΆΦ3Θ§Β±ΒψP‘ΎΒψMœ¬ΖΫ ±Θ§Φ¥tΘΦ0ΜρtΘΨ3 ±Θ§
PM=t2©¹2t©¹3©¹Θ®t©¹3Θ©Θ§
ΓύS= ![]() PMΓΝQF=
PMΓΝQF= ![]() Θ®t2©¹3tΘ©=
Θ®t2©¹3tΘ©= ![]() t2©¹
t2©¹ ![]() t
t
ΓΨΫβΈωΓΩΘ®1Θ©œ»Ϋβ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΘ§»ΜΚσ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΫβΈω ΫΘΜΘ®2Θ©œ»ΫβΖΫ≥Χ«σ≥ω≈ΉΈοœΏ”κx÷αΒΡΫΜΒψΘ§‘Ό≈–Εœ≥ωΓςBOCΚΆΓςBEDΕΦ «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§¥”ΕχΒΟΒΫΫα¬έΘΜΘ®3Θ©œ»«σ≥ωQF=1Θ§‘ΌΖ÷ΝΫ÷÷«ιΩωΘ§Β±ΒψP‘ΎΒψM…œΖΫΚΆœ¬ΖΫΘ§Ζ÷±πΦΤΥψΦ¥Ω…Θ°¥ΥΧβ «Εΰ¥ΈΚ· ΐΉέΚœΧβΘ§÷ς“ΣΩΦ≤ιΝΥ“Μ‘ΣΕΰ¥ΈΖΫ≥ΧΒΡΫβΖ®Θ§¥ΐΕ®œΒ ΐΖ®«σΚ· ΐΫβΈω ΫΘ§Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΚΆ≈–Ε®Θ§Ϋβ±ΨΧβΒΡΙΊΦϋ «≈–Ε®ΓςBCD «÷±Ϋ«»ΐΫ«–ΈΘ°


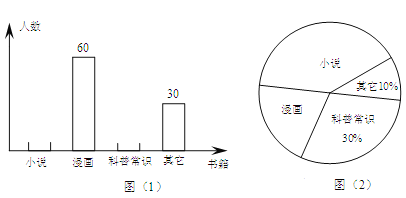
 »Ϊ”≈≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
»Ϊ”≈≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ ”Δ≤≈ΒψΫρœΒΝ–¥πΑΗ
”Δ≤≈ΒψΫρœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΒψAΘ§C‘ΎEF…œΘ§ADΓΈBCΘ§DEΓΈBFΘ§AEΘΫCF.
(1)«σ÷ΛΘΚΥΡ±Ώ–ΈABCD «ΤΫ––ΥΡ±Ώ–ΈΘΜ
(2)÷±Ϋ”–¥≥ωΆΦ÷–Υυ”–œύΒ»ΒΡœΏΕΈ(AEΘΫCF≥ΐΆβ)Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΪ«ζœΏ![]() Θ®xΘΦ0Θ©Ψ≠ΙΐΤΫ––ΥΡ±Ώ–ΈABCOΒΡΕ‘Ϋ«œΏΫΜΒψDΘ§“―÷Σ±ΏOC‘Ύy÷α…œΘ§«“ACΓΆAB”ΎΒψCΘ§‘ρΤΫ––ΥΡ±Ώ–ΈABCOΒΡΟφΜΐ «Θ®ΓΓΓΓΘ©
Θ®xΘΦ0Θ©Ψ≠ΙΐΤΫ––ΥΡ±Ώ–ΈABCOΒΡΕ‘Ϋ«œΏΫΜΒψDΘ§“―÷Σ±ΏOC‘Ύy÷α…œΘ§«“ACΓΆAB”ΎΒψCΘ§‘ρΤΫ––ΥΡ±Ώ–ΈABCOΒΡΟφΜΐ «Θ®ΓΓΓΓΘ©

A. ![]() B.
B. ![]() C. 3 D. 6
C. 3 D. 6
ΓΨ¥πΑΗΓΩA
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΓΏΒψDΈΣΤΫ––ΥΡ±Ώ–ΈABCOΒΡΕ‘Ϋ«œΏΫΜΒψΘ§ΥΪ«ζœΏyΘΫ![]() Θ®xΘΦ0Θ©Ψ≠ΙΐΒψDΘ§ACΓΆy÷αΘ§
Θ®xΘΦ0Θ©Ψ≠ΙΐΒψDΘ§ACΓΆy÷αΘ§
ΓύSΤΫ––ΥΡ±Ώ–ΈABCOΘΫ4SΓςCODΘΫ4ΓΝ![]() ΓΝ|
ΓΝ|![]() |ΘΫ
|ΘΫ![]() Θ°
Θ°
Ι ―ΓAΘ°
ΒψΨΠΘΚ±ΨΧβΩΦ≤ιΝΥΖ¥±»άΐΚ· ΐœΒ ΐkΒΡΦΗΚΈ“β“ε“‘ΦΑΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ Θ§ΗυΨίΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ ΫαΚœΖ¥±»άΐΚ· ΐœΒ ΐkΒΡΦΗΚΈ“β“εΘ§’“≥ωSΤΫ––ΥΡ±Ώ–ΈABCOΘΫ4SΓςCODΘΫ2|k| «ΫβΧβΒΡΙΊΦϋΘ°
ΓΨΧβ–ΆΓΩΒΞ―ΓΧβ
ΓΨΫα χΓΩ
9
ΓΨΧβΡΩΓΩ»γΙϊΖ÷ Ϋ![]() ‘Ύ Β ΐΖΕΈßΡΎ”–“β“εΘ§‘ρ
‘Ύ Β ΐΖΕΈßΡΎ”–“β“εΘ§‘ρ![]() ΒΡ»Γ÷ΒΖΕΈß «_____________.
ΒΡ»Γ÷ΒΖΕΈß «_____________.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2016Ρξ2‘¬1»’Θ§Έ“Ιζ‘ΎΈς≤ΐΈά–«ΖΔ…δ÷––ΡΘ§”Ο≥Λ’ς»ΐΚ≈±ϊ‘Υ‘ΊΜπΦΐ≥…ΙΠΫΪΒΎ5Ω≈–¬“Μ¥ζ±±ΕΖ–«ΥΆ»κ‘ΛΕ®ΙλΒάΘ§»γΆΦΘ§ΜπΦΐ¥”ΒΊΟφL¥ΠΖΔ…δΘ§Β±ΜπΦΐ¥οΒΫAΒψ ±Θ§¥”ΈΜ”ΎΒΊΟφR¥ΠάΉ¥ο’Ψ≤βΒΟARΒΡΨύάκ «6kmΘ§―ωΫ«ΈΣ42.4ΓψΘΜ1ΟκΚσΜπΦΐΒΫ¥οBΒψΘ§¥Υ ±≤βΒΟ―ωΫ«ΈΣ45.5Γψ
Θ®1Θ©«σΖΔ…δΧ®”κάΉ¥ο’Ψ÷°ΦδΒΡΨύάκLRΘΜ
Θ®2Θ©«σ’βΟΕΜπΦΐ¥”AΒΫBΒΡΤΫΨυΥΌΕ» «Εύ…ΌΘ®ΫαΙϊΨΪ»ΖΒΫ0.01Θ©ΘΩ
Θ®≤ΈΩΦ ΐΨίΘΚson42.4ΓψΓ÷0.67Θ§cos42.4ΓψΓ÷0.74Θ§tan42.4ΓψΓ÷0.905Θ§sin45.5ΓψΓ÷0.71Θ§cos45.5ΓψΓ÷0.70Θ§tan45.5ΓψΓ÷1.02 Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΙΊ”ΎxΒΡΖ÷ ΫΖΫ≥Χ ![]() ΈόΫβΘ§‘ρmΒΡ÷ΒΈΣ_______Θ°
ΈόΫβΘ§‘ρmΒΡ÷ΒΈΣ_______Θ°
ΓΨ¥πΑΗΓΩ-4Θ§-6
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚ»ΞΖ÷ΡΗΒΟΘΚx(mΘΪ2x)Θ≠2x(xΘ≠3)ΘΫ2(xΘ≠3)Θ§
(mΘΪ4)xΘΫΘ≠6Θ§
Β±mΘΪ4ΓΌ0 ±Θ§
xΘΫ![]() ΓΌ0Θ§
ΓΌ0Θ§
ΓΏΖ÷ ΫΖΫ≥ΧΈόΫβΘ§
ΓύxΘ≠3ΘΫ![]() Θ≠3ΘΫ0Θ§
Θ≠3ΘΫ0Θ§
ΫβΒΟΘΚmΘΫΘ≠6ΘΜ
Β±mΘΪ4ΘΫ0Φ¥mΘΫΘ≠4 ±Θ§
’ϊ ΫΖΫ≥ΧΈόΫβΘ§Ζ÷ ΫΖΫ≥Χ“≤ΈόΫβΘ§ΖϊΚœΧβ“βΘ§
Ι mΒΡ÷ΒΈΣΘ≠4ΜρΘ≠6Θ°
Ι ¥πΑΗΈΣΘΚΘ≠4ΜρΘ≠6Θ°
ΓΨΧβ–ΆΓΩΧνΩ’Χβ
ΓΨΫα χΓΩ
19
ΓΨΧβΡΩΓΩΦΤΥψ:
Θ®1Θ©![]() (2)
(2) ![]()
(3) ![]() (4)
(4) 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβ―ß…ζΩΈΆβ‘ΡΕΝΒΡœ≤ΚΟΘ§Ρ≥–Θ¥”ΑΥΡξΦΕΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––Έ ΨμΒς≤ιΘ§Βς≤ι“Σ«σΟΩ»Υ÷̯ûÓΜ÷÷œ≤ΜΕΒΡ ιΦ°Θ§»γΙϊΟΜ”–œ≤ΜΕΒΡ ιΦ°Θ§‘ρΉςΓΑΤδΥϋΓ±άύΆ≥ΦΤΓΘΆΦΘ®1Θ©”κΆΦΘ®2Θ© «’ϊάμ ΐΨίΚσΜφ÷ΤΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΓΘ“‘œ¬Ϋα¬έ≤Μ’ΐ»ΖΒΡ «Θ® Θ©
A. ”…’βΝΫΗωΆ≥ΦΤΆΦΩ…÷Σœ≤ΜΕΓΑΩΤΤ’≥Θ ΕΓ±ΒΡ―ß…ζ”–90»ΥΘ°
B. »τΗΟΡξΦΕΙ≤”–1200Οϊ―ß…ζΘ§‘ρ”…’βΝΫΗωΆ≥ΦΤΆΦΩ…ΙάΦΤœ≤Α°ΓΑΩΤΤ’≥Θ ΕΓ±ΒΡ―ß…ζ‘Φ”–360ΗωΘ°
C. ”…’βΝΫΗωΆ≥ΦΤΆΦ≤ΜΡή»ΖΕ®œ≤ΜΕΓΑ–ΓΥΒΓ±ΒΡ»Υ ΐΘ°
D. ‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§ΓΑ¬ΰΜ≠Γ±Υυ‘Ύ…»–ΈΒΡ‘≤–ΡΫ«ΈΣ72ΓψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣA(Θ≠4Θ§n)ΓΔB(3Θ§4) «“Μ¥ΈΚ· ΐy1ΘΫkxΘΪbΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐ![]() ΒΡΆΦœσΒΡΝΫΗωΫΜΒψΘ§ΙΐΒψD(tΘ§0)Θ®0ΘΦtΘΦ3Θ©Ήςx÷αΒΡ¥ΙœΏΘ§Ζ÷±πΫΜΥΪ«ζœΏ
ΒΡΆΦœσΒΡΝΫΗωΫΜΒψΘ§ΙΐΒψD(tΘ§0)Θ®0ΘΦtΘΦ3Θ©Ήςx÷αΒΡ¥ΙœΏΘ§Ζ÷±πΫΜΥΪ«ζœΏ![]() ΚΆ÷±œΏy1ΘΫkxΘΪb”ΎPΓΔQΝΫΒψ
ΚΆ÷±œΏy1ΘΫkxΘΪb”ΎPΓΔQΝΫΒψ
(1) ÷±Ϋ”–¥≥ωΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡΫβΈω Ϋ
(2) Β±tΈΣΚΈ÷Β ±Θ§SΓςBPQΘΫ![]() SΓςAPQ
SΓςAPQ
(3) “‘PQΈΣ±Ώ‘Ύ÷±œΏPQΒΡ”“≤ύΉς’ΐΖΫ–ΈPQMNΘ§ ‘ΥΒΟςΘΚ±ΏQM”κΥΪ«ζœΏ![]() Θ®xΘΨ0Θ© Φ÷’”–ΫΜΒψ
Θ®xΘΨ0Θ© Φ÷’”–ΫΜΒψ
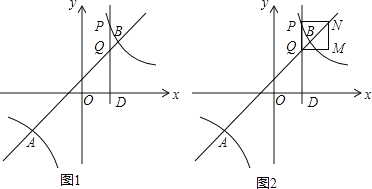
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΨΊ–ΈABCD÷–Θ§AB= ![]() Θ§BC=
Θ§BC= ![]() Θ§ΒψE‘ΎΕ‘Ϋ«œΏBD…œΘ§«“BE=1.8Θ§Ν§Ϋ”AE≤Δ―”≥ΛΫΜDC”ΎΒψFΘ§‘ρ
Θ§ΒψE‘ΎΕ‘Ϋ«œΏBD…œΘ§«“BE=1.8Θ§Ν§Ϋ”AE≤Δ―”≥ΛΫΜDC”ΎΒψFΘ§‘ρ ![]() = Θ°
= Θ° 
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΒΊΨ”Οώ…ζΜν”ΟΒγΜυ±ΨΦέΗώΈΣΟΩΕ»Βγ0.4‘ΣΘ§»τΟΩ‘¬”ΟΒγΝΩ≤Μ≥§Ιΐ![]() Ε» ±Θ§Α¥Μυ±ΨΦέΗώ ’Ζ―ΘΜ»τ≥§Ιΐ
Ε» ±Θ§Α¥Μυ±ΨΦέΗώ ’Ζ―ΘΜ»τ≥§Ιΐ![]() Ε»Θ§≥§≥ω≤ΩΖ÷Α¥Μυ±ΨΦέΗώΒΡ150% ’Ζ―.
Ε»Θ§≥§≥ω≤ΩΖ÷Α¥Μυ±ΨΦέΗώΒΡ150% ’Ζ―.
Θ®1Θ©Ρ≥Μß8‘¬Ζί”ΟΒγ84Ε»Θ§Ι≤ΫΜΒγΖ―38.4‘ΣΘ§«σ![]() ΒΡ÷ΒΓΘ
ΒΡ÷ΒΓΘ
Θ®2Θ©»γΙϊΗΟΜß9‘¬ΖίΒΡΒγΖ―ΤΫΨυΈΣΟΩΕ»0.5‘ΣΘ§Ρ«Ο¥ΗΟ”ΟΜß9‘¬Ζί”ΟΒγΕύ…ΌΕ»ΘΩ”ΠΫΜΒγΖ―Εύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com