
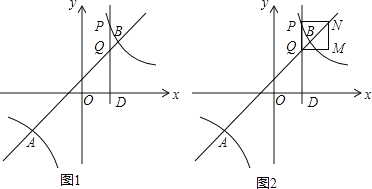
����Ŀ����ͼ����֪A(��4��n)��B(3��4)��һ�κ���y1��kx��b��ͼ���뷴��������![]() ��ͼ����������㣬����D(t��0)��0��t��3����x��Ĵ��ߣ��ֱ�˫����
��ͼ����������㣬����D(t��0)��0��t��3����x��Ĵ��ߣ��ֱ�˫����![]() ��ֱ��y1��kx��b��P��Q����
��ֱ��y1��kx��b��P��Q����
(1) ֱ��д��������������һ�κ����Ľ���ʽ
(2) ��tΪ��ֵʱ��S��BPQ��![]() S��APQ
S��APQ
(3) ��PQΪ����ֱ��PQ���Ҳ���������PQMN����˵������QM��˫����![]() ��x��0��ʼ���н���
��x��0��ʼ���н���
���𰸡���1��![]() ����2��
����2��![]() ����3��������
����3��������
�������������������1�����ݵ�B��������÷�������������ʽ���ٸ��ݷ�����������õ�A�����꣬�����ݴ���ϵ�������һ�κ�������ʽ���ɣ�
��2����APQ���BPQ��һ�������ߣ�����ͬ�������ε����֮�ȵ��ڸ�֮�ȣ��г�����t�ķ��̽�����⣻
��3����ֱ��QM��˫���߽���C�㣬���ݵ�P��Q��C��������꣬��t�Ĵ���ʽ��ʾ��QM-QC���ٸ���t��ȡֵ��Χ�жϴ���ʽ��ֵ�ķ��ż��ɣ�
���������
��1����B��3��4������![]() ����m=3��4=12��
����m=3��4=12��
�෴������������ʽΪ![]() ��
��
��A����4��n�����뷴������������n=��3��
��A����4����3��
��ֱ��y1=kx+b����A�͵�B��
��![]() �����
�����![]() ��
��
��һ�κ����Ľ���ʽΪy=x+1��
��2����ͼ1����PQ��x�ᣬ
����PQΪ�ױ�ʱ����APQ���BPQ�����֮�ȵ���PQ���ϵĸ�֮�ȣ�
�֡�![]() ��
��
��![]() ��
��
�ߵ�D��t��0����A����4����3����B��3��4����
�� ����
����![]() ��
��
���![]() ��
��
��3����ͼ2����ֱ��QM��˫���߽���C�㣮
�������֪��P��t��![]() ����Q��t��t+1����C��
����Q��t��t+1����C��![]() ��t+1����
��t+1����
��QM=PQ=![]() ��QC=
��QC=![]() ��
��
��QM��QC=![]() =
=![]() ��
��
��0��t��3��
��0��t��t+1����12��
��![]() ��1��
��1��
��QM��QC��0��
��QM��QC��
����QM��˫����![]() ʼ���н��㣮
ʼ���н��㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ͼ���У�����������ͼ���ܽ��Ƶؿ̻�����![]() �����龳��
�����龳��
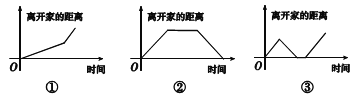
�龳![]() ��С���뿪�Ҳ��ã����ְ���ҵ�����ڼ�����Ƿ��ؼ����ҵ�����ҵ����ȥѧУ��
��С���뿪�Ҳ��ã����ְ���ҵ�����ڼ�����Ƿ��ؼ����ҵ�����ҵ����ȥѧУ��
�龳![]() ��С���Ӽҳ���������һ��·�̺�Ϊ�˸�ʱ�䣬�Ը�����ٶ�ǰ��.
��С���Ӽҳ���������һ��·�̺�Ϊ�˸�ʱ�䣬�Ը�����ٶ�ǰ��.
��1���龳![]() ��
�� ![]() ����Ӧ�ĺ���ͼ��ֱ�Ϊ������������������д��ţ���
����Ӧ�ĺ���ͼ��ֱ�Ϊ������������������д��ţ���
��2������Ϊʣ�µĺ���ͼ��д��һ���ʺϵ��龳��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ֱ��y=kx(k<0)��˫����![]() ����A(x1��y1)��B(x2��y2)����,��3x1y2-5x2y1��ֵΪ __________.
����A(x1��y1)��B(x2��y2)����,��3x1y2-5x2y1��ֵΪ __________.

���𰸡�-6
������������������ߵ�A��x1��y1����B��x2��y2����˫����y��![]() �ϵĵ㣬
�ϵĵ㣬
��x1y1��x2y2����3����
��ֱ��y��kx��k��0����˫����y��![]() ���ڵ�A��x1��y1����B��x2��y2�����㣬
���ڵ�A��x1��y1����B��x2��y2�����㣬
��x1����x2��y1����y2����
��ԭʽ����3x1y1��5x2y2��9��15����6��
�ʴ�Ϊ����6��
�㾦�����⿼����Ƿ�����������һ�κ����Ľ������⣬�����������ĶԳ��ԣ����ݷ�����������ͼ�����ԭ��ԳƵó�x1����x2��y1����y2�ǽ�����Ĺؼ���
�����͡������
��������
15
����Ŀ��A��B�������180km�����ĸ��ٹ�·��ͨ����A��B���ؼ���ʻ�ij�;�ͳ�ƽ����������� 50%������A�ص�B�ص�ʱ�������� 1h .����ԭ����ƽ������Ϊxkm/h�������������з���Ϊ _____________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��m��n��һԪ���η���x2+4x+3=0������ʵ��������|m|��|n|��������y=x2+bx+c��ͼ����A��m��0����B��0��n������ͼ��ʾ��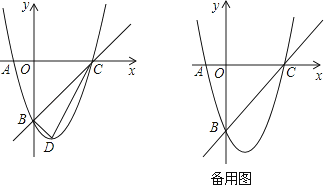
��1������������ߵĽ���ʽ��
��2���裨1���е���������x�����һ������Ϊ�����ߵĶ���ΪD���������C��D�����꣬���жϡ�BCD����״��
��3����P��ֱ��BC�ϵ�һ�����㣨��P�����B�͵�C�غϣ�������P��x��Ĵ��ߣ����������ڵ�M����Q��ֱ��BC�ϣ������PΪ ![]() ����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
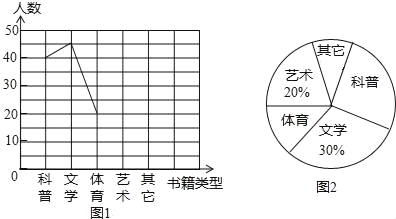
����Ŀ��2016��3�£�ij��ѧ�ԡ�ÿ���Ķ�lСʱ��Ϊ���⣬��ѧ����ϲ�����鼮���ͽ�������������飬�ռ��������ݺ��Ƴ���������δ��ɵ�ͳ��ͼ�������ͼ1��ͼ2�ṩ����Ϣ������������⣺
��1���������ͳ��ͼ��ͼ1������������
��2�����������ѧ����ѧ��900������ô���������ϲ���������鼮��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
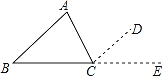
����Ŀ����֪����ABC����A����B����C֮��Ϊ���٣�Ϊʲô��
������A+��B+��C=180��
���ɣ�����ACD=��A�����ӳ�BC��E
�ߡ�ACD=���� ����������
AB��CD���� ����
���B=�� ������ ����
����ACB+��ACD+��DCE=180��
���ACB+�� ��+�� ��=180�㣨�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ�������ε��ڽǺ�ʱ��������һ���ڽǵĶ���������ڽǺ�Ϊ1 560�㣬������ڽ��Ƕ��ٶȣ��������εı����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���г���һ�ܼƻ�����1400�����г���ƽ��ÿ������200�������ڸ���ԭ��ʵ��ÿ����������ƻ�������г���![]() ����ij�ܵ��������
����ij�ܵ��������![]() ����Ϊ��������Ϊ��
��������������![]() ��
��
���� | һ | �� | �� | �� | �� | �� | �� |
���� |
|
|
|
|
|
|
|
![]() ���ݼ�¼��֪ǰ���칲������������
���ݼ�¼��֪ǰ���칲������������
![]() ��������һ��Ȳ������ٵ�һ���������������
��������һ��Ȳ������ٵ�һ���������������
![]() �ó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ�����ɵ�60Ԫ���������������������ÿ������15Ԫ��������һ����15Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�
�ó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ�����ɵ�60Ԫ���������������������ÿ������15Ԫ��������һ����15Ԫ����ô�ó�������һ�ܵĹ����ܶ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��FC��D��AB��һ�㣬DF��AC�ڵ�E��DE=FE���ֱ��ӳ�FD��CB���ڵ�G�� 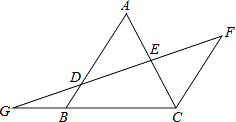
��1����֤����ADE�ա�CFE��
��2����GB=2��BC=4��BD=1����AB�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com