
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 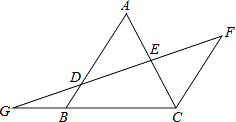
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
【答案】
(1)证明:∵AB∥FC,
∴∠A=∠FCE,
在△ADE和△CFE中,
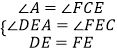 ,
,
∴△ADE≌△CFE(AAS)
(2)解:∵AB∥FC,
∴△GBD∽△GCF,
∴GB:GC=BD:CF,
∵GB=2,BC=4,BD=1,
∴2:6=1:CF,
∴CF=3,
∵AD=CF,
∴AB=AD+BD=4
【解析】(1)由平行线的性质可得:∠A=∠FCE,再根据对顶角相等以及全等三角形的判定方法即可证明:△ADE≌△CFE;(2)由AB∥FC,可证明△GBD∽△GCF,根据给出的已知数据可求出CF的长,即AD的长,进而可求出AB的长.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
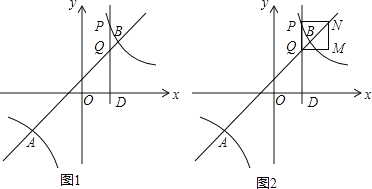
【题目】如图,已知A(-4,n)、B(3,4)是一次函数y1=kx+b的图象与反比例函数![]() 的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线
的图象的两个交点,过点D(t,0)(0<t<3)作x轴的垂线,分别交双曲线![]() 和直线y1=kx+b于P、Q两点
和直线y1=kx+b于P、Q两点
(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时,S△BPQ=![]() S△APQ
S△APQ
(3) 以PQ为边在直线PQ的右侧作正方形PQMN,试说明:边QM与双曲线![]() (x>0)始终有交点
(x>0)始终有交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
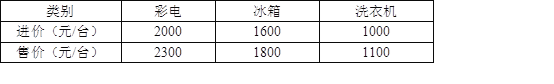
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地居民生活用电基本价格为每度电0.4元,若每月用电量不超过![]() 度时,按基本价格收费;若超过
度时,按基本价格收费;若超过![]() 度,超出部分按基本价格的150%收费.
度,超出部分按基本价格的150%收费.
(1)某户8月份用电84度,共交电费38.4元,求![]() 的值。
的值。
(2)如果该户9月份的电费平均为每度0.5元,那么该用户9月份用电多少度?应交电费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=68°,∠2=68°,∠3=112°.在下列解答中,填空:
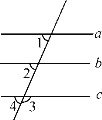
(1)因为∠1=68°,∠2=68°(已知),
所以__________(等量代换).
所以____∥_____________________________.
(2)因为∠3+∠4=180°(邻补角的定义),∠3=112°
,所以____________
又因为∠2=68°,
所以___________(等量代换),
所以____∥_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直径为200cm的圆柱形油槽内装入一些油以后,截面如图.若油面的宽AB=160cm,则油的最大深度为( ) 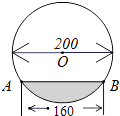
A.40cm
B.60cm
C.80cm
D.100cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的小正方形纸片,按下图的方式拼正方形:
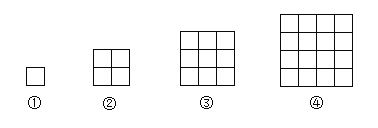
规律:第①个图形中有1个小正方形;
第②个图形比第①个图形多3个小正方形;
第③个图形比第②个图形多5个小正方形;……
第(n+1)个图形比第n个图形多________个小正方形;
可发现以下结论:(1)1+3+5+……+(2n-1)= ____________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8),求点E的坐标
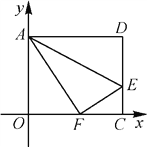
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com