
【题目】用同样大小的小正方形纸片,按下图的方式拼正方形:
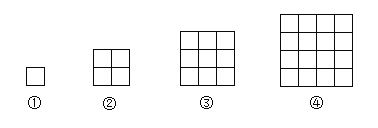
规律:第①个图形中有1个小正方形;
第②个图形比第①个图形多3个小正方形;
第③个图形比第②个图形多5个小正方形;……
第(n+1)个图形比第n个图形多________个小正方形;
可发现以下结论:(1)1+3+5+……+(2n-1)= ____________;
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入![]() 表是某周的生产情况
表是某周的生产情况![]() 超产为正、减产为负
超产为正、减产为负![]() :
:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产多少辆;
根据记录可知前三天共生产多少辆;
![]() 产量最多的一天比产量最少的一天多生产多少辆;
产量最多的一天比产量最少的一天多生产多少辆;
![]() 该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 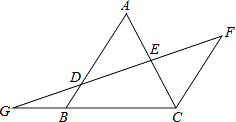
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,D是BC边上的一个动点(点D不与B,C重合)△ADF是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.

(1)如图1,求证:△AFB≌△ADC;
(2)请判断图1中四边形BCEF的形状,并说明理由;
(3)若D点在BC 边的延长线上,如图2,其它条件不变,请问(2)中结论还成立吗?如果成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,垂足为点E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.
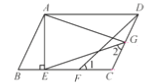
(1)若CF=2,AE=3,求BE的长;
(2)求证:∠CEG=![]() ∠AGE.
∠AGE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 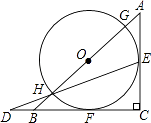
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB、CD之间有一动点P,满足0°<∠EPF<180°.



(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB、CD之间有一动点,因此需要对点P的位置进行分类讨论;如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________。
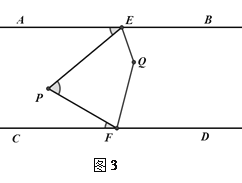
(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF=_______°.
②猜想∠EPF与∠EQF的数量关系,并说明理由.
③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,此次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. 
(1)如图1,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD为△ABC的完美分割线.
(2)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且△ACD为等腰三角形,求∠ACB的度数.
(3)如图2,△ABC中,AC=2,BC= ![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,某校规定学生每天参加户外活动的平均时间不少于1小时,为了解学生参加户外活动的情况,对该校七年级部分学生参加户外活动的时间进行调查,并将调查结果绘制成如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:

(1)填空:这次调查的学生共 人,表示户外活动时间为1小时的扇形圆心角度数是 度;
(2)求参加户外活动的时间为1.5小时的学生人数,并补全频数分布直方图;
(3)若该校七年级有学生600人,请估计该校七年级学生参加户外活动的时间不少于1小时的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com