
����Ŀ����ͼ��AB��CD������E��F�ֱ���ֱ��AB��CD�ϣ���ƽ����AB��CD֮����һ����P������0��<��EPF<180��.


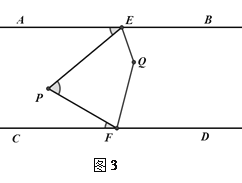

��1�����ʡ�AEP����EPF����PFC����������������ϵ��
�⣺���ڵ�P��ƽ����AB��CD֮����һ���㣬�����Ҫ�Ե�P��λ�ý��з������ۣ���ͼ1����P����EF�����ʱ����AEP����EPF����PFC����������ϵΪ______________����ͼ2����P����EF���Ҳ�ʱ����AEP����EPF����PFC����������ϵΪ______________��
��2����ͼ3��QE��QF�ֱ�ƽ�֡�PEB�͡�PFD���ҵ�P��EF���.
������EPF=60�㣬���EQF=_______��.
�ڲ����EPF���EQF��������ϵ����˵������.
����ͼ4������BEQ���DFQ�Ľ�ƽ���߽��ڵ�Q1����BEQ1���DFQ1�Ľ�ƽ���߽��ڵ�Q2����BEQ2���DFQ2�Ľ�ƽ���߽��ڵ�Q3���˴����ƣ����EPF���EQ2018F����������������ϵ����ֱ��д�������
���𰸡���1����AEP+��PFC=��EPF����AEP+��PFC+��EPF=360�㣻
��2����150��
�ڡ�EPF���EQF��������ϵΪ��EPF+2��EQF=360�㣬�������������
�ۡ�EPF+22019��EQ2018F=360��.
��������
��1����ͼ1������P��PH��AB��֤�� AB��PH��CD��Ȼ�����ƽ���ߵ�����֤�ý��ۣ���ͼ2������P��PH��AB��֤��AB��PH��CD ��Ȼ�����ƽ���ߵ�����֤�ý��ۣ�
��2������ͼ3������P��PH��AB������Q��QG��AB��Ȼ�����ƽ���ߵ����ʵõ���EPF=��AEP+��CFP����EQF=��BEQ+��DFQ ���ɡ�EPF=60�㣬QE��QF�ֱ�ƽ�֡�PEB�͡�PFD��������ý��ۣ�
��ͬ�ټ��ɵý��ۣ�
���ɣ�2����֪��EPF+2��EQF=360�㣬������EPF+22��EQ1F=360�㣬
��EPF+23��EQ2F=360�����ɹ��ɼ�����ý���.
��1����ͼ1������P��PH��AB��
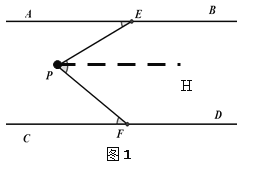
��AB��CD��PH��AB����AB��PH��CD��
���AEP=��EPH����PFC=��FPH��
�ߡ�EPF=��EPH+��FPH��
���EPF=��AEP+��PFC��
��ͼ2������P��PH��AB��
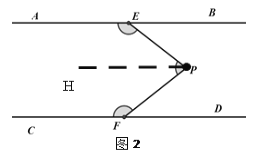
��AB��CD��PH��AB��
��AB��PH��CD��
���AEP+��EPH=180�㣬��CFP+��FPH=180�㣬
�ߡ�EPF=��EPH+��FPH��
���AEP+��PFC+��EPF=360��.
�ʴ�Ϊ��AEP+��PFC=��EPF����AEP+��PFC+��EPF=360�㣻
��2������ͼ3������P��PH��AB������Q��QG��AB��
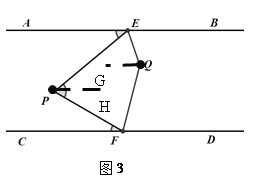
��AB��CD��PH��AB��
��AB��PH��CD��
���AEP=��EPH����PFC=��FPH��
�ߡ�EPF=��EPH+��FPH��
���EPF=��AEP+��PFC��
ͬ������EQF=��BEQ+��DFQ��
�ߡ�EPF=60�㣬
���AEP+��PFC=60�㣬
���BEP+��DEP=300�㣬
��QE��QF�ֱ�ƽ����PEB����PFD��
���BEQ+��DFQ=150��,
���EQF=150�㣻
��2���ڡ�EPF����EQF��������ϵΪ��EPF+2��EQF=360�㣬
���ɣ�
����1������2������֪��EPF+��BEP+��DFP=360�㣬��EQF=��BEQ+��DFQ��
��QE��QF�ֱ�ƽ����PEB����PFD��
���BEP=2��BEQ����DFP=2��DFQ��
���BEP+��DFP=2����BEQ+��DFQ��=2��EQF��
���EPF+2��EQF=360�㣻
��3���ɣ�2����֪��EPF+2��EQF=360�㣬
ͬ����֤����EPF+22��EQ1F=360�㣬
��EPF+23��EQ2F=360�㣬
����
��EPF+22019��EQ2018F=360�㣬
�ʴ�Ϊ��EPF+22019��EQ2018F=360��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣������ڼ䣬Ϊ��������յ���������ij�̵�ƻ���170000Ԫ����һ���ҵ磬�����ҵ�Ľ��ۺ��ۼ������
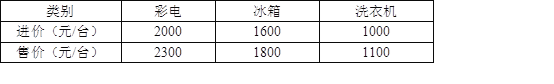
���������ʽ������ķ�Χ�ڣ������������ҵ繲100̨�����вʵ�̨���DZ���̨����2��������̵깺�����x̨��
��1���̵�������Թ���������̨��
��2������������̨ʱ����ʹ�̵������������ҵ���õ���������������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��Ϊ200cm��Բ�����Ͳ���װ��һЩ���Ժ�����ͼ��������Ŀ�AB=160cm�����͵�������Ϊ�� �� 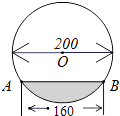
A.40cm
B.60cm
C.80cm
D.100cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬ����С��С������ֽƬ������ͼ�ķ�ʽƴ��������
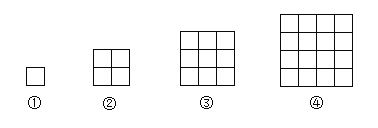
���ɣ��ڢٸ�ͼ������1��С�����Σ�
�ڢڸ�ͼ�αȵڢٸ�ͼ�ζ�3��С�����Σ�
�ڢ۸�ͼ�αȵڢڸ�ͼ�ζ�5��С�����Σ�����
��(n+1)��ͼ�αȵ�n��ͼ�ζ�________��С��������
�ɷ������½��ۣ���1��1+3+5+����+��2n��1��= ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�洬�����������У���A���ú���Cλ�ڱ�ƫ��60��ķ���ǰ��20���ﵽ��B�㣬��ʱ����ú���Cλ�ڱ�ƫ��30��ķ�����C������AB�ľ���CD�������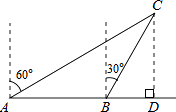
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽��ũ����Ů��ѧ�ѵ����⣬���н�����һ����ũ����Ů��ѧ�ı��ϻ��ƣ�����һ������⽻�������������ͳ�ƣ�2004���^��![]() ��ũ����Ů������������Сѧѧϰ��Ԥ��2005���^������������Сѧѧϰ��ũ����Ů��2004���������ӣ�����Сѧ����
��ũ����Ů������������Сѧѧϰ��Ԥ��2005���^������������Сѧѧϰ��ũ����Ů��2004���������ӣ�����Сѧ����![]() ����ѧ����
����ѧ����![]() ��������2005���^������
��������2005���^������![]() ��ũ����Ů����������Сѧѧϰ��
��ũ����Ů����������Сѧѧϰ��
��1�������Сѧÿ��ÿ�������������![]() Ԫ����ѧÿ��ÿ�������������
Ԫ����ѧÿ��ÿ�������������![]() Ԫ���㣬��2005�������ӵ�
Ԫ���㣬��2005�������ӵ�![]() ����Сѧѧ�������ն��������������
����Сѧѧ�������ն��������������
��2�����Сѧÿ����![]() ��ѧ�����䱸
��ѧ�����䱸![]() ����ʦ����ѧÿ����
����ʦ����ѧÿ����![]() ��ѧ�����䱸
��ѧ�����䱸![]() ����ʦ������2005���^��ѧ��ũ����Ů����������Сѧ�Ͷ���ѧ�����ӵ��������㣬һ����Ҫ�䱸��������Сѧ��ʦ��
����ʦ������2005���^��ѧ��ũ����Ů����������Сѧ�Ͷ���ѧ�����ӵ��������㣬һ����Ҫ�䱸��������Сѧ��ʦ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㡣
��1�����㣺 ![]() +����3��2����
+����3��2���� ![]() ��1��0 ��
��1��0 ��
��2������2+m����2��m��+m��m��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������AOCD��ֱ��AE�۵�(��E�ڱ�DC��)���۵���Dǡ�����ڱ�OC�ϵĵ�F��������D������Ϊ(10��8)�����E������
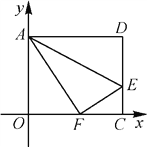
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һֻ�����ĺ������б�����ȫ��ͬ�������Ϸֱ�д������1��2��3��4�����ſ�Ƭ��С����������س�ȡһ�ţ��ѿ�Ƭ�ϵ�������Ϊ������������һֻ�����ĺ����ォ��״����С��ȫ��ͬ���ֱ��������1��2��3������С���Ϻ�С����������س�ȡһ������С���ϵ�������Ϊ������Ȼ���������������IJ
��1�������û���״ͼ���б��ķ���������������Ϊ0�ĸ��ʣ�
��2��С����С������Ϸ�������ǣ����������IJ�Ϊ����������С��Ӯ������С��Ӯ������Ϊ����Ϸ��ƽ����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com