
【题目】(10分)国庆期间,为了满足百姓的消费需求,某商店计划用170000元购进一批家电,这批家电的进价和售价如表:
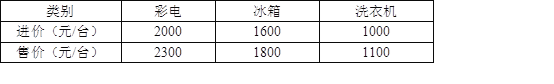
若在现有资金允许的范围内,购买表中三类家电共100台,其中彩电台数是冰箱台数的2倍,设该商店购买冰箱x台.
(1)商店至多可以购买冰箱多少台?
(2)购买冰箱多少台时,能使商店销售完这批家电后获得的利润最大?最大利润为多少元?
【答案】(1)26;(2)购买冰箱26台时,能使商店销售完这批家电后获得的利润最大,最大利润为23000元.
【解析】试题分析:(1)根据三种家电的总进价小于等于170000元列出关于x的不等式,由x为正整数,即可得到答案;
(2)设商店销售完这批家电后获得的利润为y元,则y=500x+10000,结合(1)中x的取值范围,利用一次函数的性质即可解答.
试题解析:(1)根据题意,得:20002x+1600x+1000(100﹣3x)≤170000,解得: ![]() ,∵x为正整数,∴x至多为26.
,∵x为正整数,∴x至多为26.
答:商店至多可以购买冰箱26台.
(2)设商店销售完这批家电后获得的利润为y元,则y=(2300﹣2000)2x+(1800﹣1600)x+(1100﹣1000)(100﹣3x)=500x+10000,∵k=500>0,∴y随x的增大而增大,∵![]() 且x为正整数,∴当x=26时,y有最大值,最大值为:500×26+10000=23000,
且x为正整数,∴当x=26时,y有最大值,最大值为:500×26+10000=23000,
答:购买冰箱26台时,能使商店销售完这批家电后获得的利润最大,最大利润为23000元.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=kx(k<0)与双曲线![]() 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.

【答案】-6
【解析】试题分析:∵点A(x1,y1),B(x2,y2)是双曲线y=![]() 上的点,
上的点,
∴x1y1=x2y2=-3①,
∵直线y=kx(k<0)与双曲线y=![]() 交于点A(x1,y1),B(x2,y2)两点,
交于点A(x1,y1),B(x2,y2)两点,
∴x1=-x2,y1=-y2②,
∴原式=-3x1y1+5x2y2=9-15=-6.
故答案为:-6.
点睛:本题考查的是反比例函数与一次函数的交点问题,反比例函数的对称性,根据反比例函数的图象关于原点对称得出x1=-x2,y1=-y2是解答此题的关键.
【题型】填空题
【结束】
15
【题目】A,B两地相距180km,新修的高速公路开通后,在A,B两地间行驶的长途客车平均车速提高了 50%,而从A地到B地的时间缩短了 1h .若设原来的平均车速为xkm/h,则根据题意可列方程为 _____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入![]() 表是某周的生产情况
表是某周的生产情况![]() 超产为正、减产为负
超产为正、减产为负![]() :
:
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
![]() 根据记录可知前三天共生产多少辆;
根据记录可知前三天共生产多少辆;
![]() 产量最多的一天比产量最少的一天多生产多少辆;
产量最多的一天比产量最少的一天多生产多少辆;
![]() 该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列各式:(ab)2=a2b2,(ab)3=a3b3,(ab)4=a4b4…
回答下列三个问题:
(1)验证:(2×![]() )100= ,2100×(
)100= ,2100×(![]() )100= ;
)100= ;
(2)通过上述验证,归纳得出:(ab)n= ; (abc)n= .
(3)请应用上述性质计算:(﹣0.125)2017×22016×42015.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将买一些乒乓球和乒乓球拍.了解信息如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元;经洽谈:甲店每买一副球拍赠一盒乒乓球;乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球x盒时,两种优惠办法各应付款多少元?(用含x的代数式表示)
(2)如果要购买15盒乒乓球时,请你去办这件事,你打算去哪家商店购买?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G. 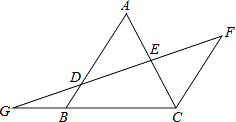
(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,定点E,F分别在直线AB,CD上,在平行线AB、CD之间有一动点P,满足0°<∠EPF<180°.



(1)试问∠AEP,∠EPF,∠PFC满足怎样的数量关系?
解:由于点P是平行线AB、CD之间有一动点,因此需要对点P的位置进行分类讨论;如图1,当P点在EF的左侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________,如图2,当P点在EF的右侧时,∠AEP,∠EPF,∠PFC满足数量关系为______________。
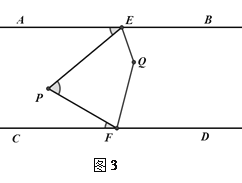
(2)如图3,QE,QF分别平分∠PEB和∠PFD,且点P在EF左侧.
①若∠EPF=60°,则∠EQF=_______°.
②猜想∠EPF与∠EQF的数量关系,并说明理由.
③如图4,若∠BEQ与∠DFQ的角平分线交于点Q1,∠BEQ1与∠DFQ1的角平分线交于点Q2,∠BEQ2与∠DFQ2的角平分线交于点Q3,此次类推,则∠EPF与∠EQ2018F满足怎样的数量关系?(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com