
����Ŀ��Ϊ�˽�ѧ�������Ķ���ϲ�ã�ijУ�Ӱ��꼶�����ȡ����ѧ�������ʾ����飬����Ҫ��ÿ��ֻѡȡһ��ϲ�����鼮�����û��ϲ�����鼮����������������ͳ�ơ�ͼ��1����ͼ��2�����������ݺ���Ƶ�������������ͳ��ͼ�����½��۲���ȷ���ǣ� ��
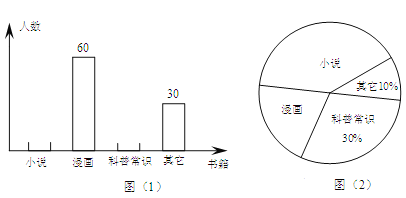
A. ��������ͳ��ͼ��֪ϲ�������ճ�ʶ����ѧ����90�ˣ�
B. �����꼶����1200��ѧ��������������ͳ��ͼ�ɹ���ϲ�������ճ�ʶ����ѧ��Լ��360����
C. ��������ͳ��ͼ����ȷ��ϲ����С˵����������
D. ������ͳ��ͼ�У����������������ε�Բ�Ľ�Ϊ72����
���𰸡�C
��������
�����������ͳ��ͼ���������η�����ѡ��������ж�.
A��ϲ�������ճ�ʶ����ѧ����30��10%��30%=90�ˣ�B�������꼶����1200��ѧ��������������ͳ��ͼ�ɹ���ϲ�������ճ�ʶ����ѧ��Լ��1200��30%=360����D��������ͳ��ͼ�У����������������ε�Բ�Ľ�Ϊ360���60����30��10%��=72��������ȷ�����������⣻
C��ϲ����С˵��������Ϊ30��10%-60-90-30=120�ˣ��ʴ���ѡ���������.


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
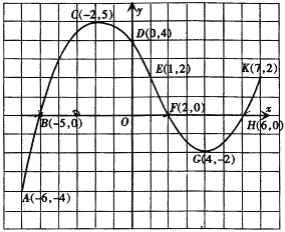
����Ŀ�����֪��������ͼ�������뺯������֮������ű�Ȼ��ϵ�������ͼ�еĺ���ͼ�����������е���ʾ��˵���˺����ı仯���ɣ����⣬�㻹��˵���˺�������Щ���ʣ�
��� | ����ͼ������ | �����仯���� |
��1�� | ���ߴӵ�A����6����4������K��7��2�� | �Ա�����ȡֵ��Χ��______�� |
��2�� | ������y�ύ�ڵ�D��0��4�� | ��x=______ʱ��y=______�� |
��3�� | ������x��ֱ��ڵ�B����5��0����F��2��0����H��6��0�� | ��x��ֵ�ֱ�Ϊ______ʱ��y=0�� |
��4�� | ���߾�����E��1��2�� | ��x=______ʱ��y=______�� |
��5�� | ������������AC������״̬ | ����6��x����2ʱ��y��x�������______�� |
��6�� | ������������CG���½�״̬ | ��______ʱ��y��x�������___________�� |
��7�� | ������������GK��____________ | ��______ʱy��____________�� |
��8�� | �����ϵ���ߵ���C����2��5�� | ��x=______ʱ��y��______ֵ�������ֵΪ____________�� |
��9�� | �����ϵ���͵���____________ | ��x=______ʱ��y��______ֵ�������ֵΪ____________�� |
��10�� | ����BCFλ��x����Ϸ� | ��______ʱ��y______0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AD=2AB=4��E��AD���е㣬һ���㹻������ǰ��ֱ�Ƕ������E�غϣ������ǰ��Ƶ�E��ת�����ǰ����ֱ�DZ߷ֱ�AB��BC�������ǵ��ӳ��ߣ��ڵ�M��N�����AEM=����0�㣼����90�㣩�����������ĸ����ۣ�
��AM=CN��
�ڡ�AME=��BNE��
��BN��AM=2��
��S��EMN= ![]() ��
��
������������ȷ�ĸ����ǣ�������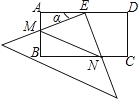
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC�����Բ��AEƽ�֡�BAC����O�ڵ�E����BC�ڵ�D������E��ֱ��l��BC��
��1���ж�ֱ��l���O��λ�ù�ϵ����˵�����ɣ�
��2������ABC��ƽ����BF��AD�ڵ�F����֤��BE=EF��
��3���ڣ�2���������£���DE=4��DF=3����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��m��n��һԪ���η���x2+4x+3=0������ʵ��������|m|��|n|��������y=x2+bx+c��ͼ����A��m��0����B��0��n������ͼ��ʾ��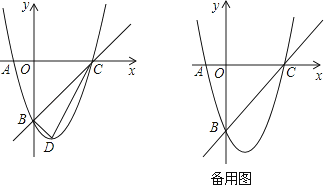
��1������������ߵĽ���ʽ��
��2���裨1���е���������x�����һ������Ϊ�����ߵĶ���ΪD���������C��D�����꣬���жϡ�BCD����״��
��3����P��ֱ��BC�ϵ�һ�����㣨��P�����B�͵�C�غϣ�������P��x��Ĵ��ߣ����������ڵ�M����Q��ֱ��BC�ϣ������PΪ ![]() ����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
����λ���ȣ����P�ĺ�����Ϊt����PMQ�����ΪS�����S��t֮��ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��˾���Ľ�ͨ��ȫ��ʶ���������ý�ͨ��ȫ�����¶�˾�������˽�ͨ��ȫ֪ʶ�ʾ����飮���ھƼ���������µ����ʾ���
�˷��Ƽݩ�������Ϊ���ַ�ʽ��ã�����ѡ�� |
A�Ӵ��������ȣ���ǿ˾�����ط���ʶ�� B��������������ܰ��ʾ��������Ƽݡ��� C˾���ϸ�ǰǩ���ܽӾƼݡ���֤�飮 D�Ӵ������ȣ���������Ƽݣ� E����Ƽ���һͬ�Ͳ��˵��������Σ� |
�����ȡ�����ʾ�������������������ͳ��ͼ��

����������Ϣ������������⣺
��1�����ε�������������Ƕ��٣�
��2����ȫ����ͼ��������Bѡ������Ӧ����Բ�ĽǵĶ�����
��3����������3000��˾�����뱾�λ����֧��Dѡ���˾����Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
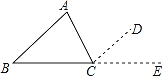
����Ŀ����֪����ABC����A����B����C֮��Ϊ���٣�Ϊʲô��
������A+��B+��C=180��
���ɣ�����ACD=��A�����ӳ�BC��E
�ߡ�ACD=���� ����������
AB��CD���� ����
���B=�� ������ ����
����ACB+��ACD+��DCE=180��
���ACB+�� ��+�� ��=180�㣨�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˶�Ա��һ����������еļ���ͳ�������ʾ��
���� | �ϳ�ʱ�䣨���ӣ� | ����Ͷ�����Σ� | Ͷ�� | ����÷� | ���� | �������Σ� | �����ܵ÷� |
���� | 46 | 66 | 22 | 10 | 11 | 8 | 60 |
ע�����г���Ͷ��������Ͷ�д���������������
����������Ϣ���������и��˶�ԱͶ��2�����3�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������û������ܾ�ð���̡���ij�й�����˾����̭ijһ����·�ϡ�ð���̡������صĹ��������ƻ�����A�ͺ�B�����ֻ������ܹ�������10����������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ��
��1������A�ͺ�B������ÿ�����������Ԫ��
��2��Ԥ���ڸ���·��A�ͺ�B������ÿ������ؿ����ֱ�Ϊ60���˴κ�100���˴Σ����ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ���ù�˾���ļ��ֹ������������ֹ��������ܷ������٣������ܷ����Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com