
【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
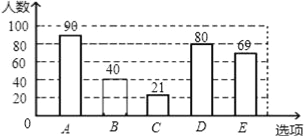
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?
【答案】(1)样本容量300 ;(2)补图见解析,48°;(3)支持D选项的司机大约有800人.
【解析】试题分析:(1)用E小组的频数除以该组所占的百分比即可求得样本容量;
(2)用总人数乘以该组所占的百分比即可求得A组的人数,总数减去其他小组的频数即可求得B小组的人数;
(3)总人数乘以支持D选项的人数占300人的比例即可;
试题解析:(1)样本容量:69÷23%=300 ;
(2)A组人数为300×30%=90(人)
B组人数:300﹣(90+21+80+69)=40(人,)
补全条形图人数为40 ,
圆心角度数为 360°×![]() =48°;
=48°;
(3)3000×![]() =800(人),
=800(人),
答:支持D选项的司机大约有800人.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元
万元![]() 其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 | 每公顷获利 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
![]() 求出茄子和西红柿的种植面积各为多少公顷?
求出茄子和西红柿的种植面积各为多少公顷?
![]() 种植场在这一季共获利多少万元?
种植场在这一季共获利多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数![]() 的图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是________.
的图象上的三点,且x1<0<x2<x3,则y1,y2,y3的大小关系是________.
【答案】![]()
【解析】试题分析:∵函数y=![]() 中,k=-1<0,
中,k=-1<0,
∴此函数的图象的两个分支位于二四象限,且在每一象限内,y随x的增大而增大.
∵x1<0<x2<x3,
∴点A(x1,y1)在第二象限,B(x2,y2)、C(x3,y3)在第四象限,
∴y1>0,y2<y3<0,
∴y2<y3<y1.
故答案为:y2<y3<y1.
点睛:本题考查的是反比例函数图象的性质,当k>0时,图象位于一三象限,在每一个象限内y随x的增大而减小,k<0时,图象位于二四象限,在每一个象限内,y随x的增大而增大.
【题型】填空题
【结束】
14
【题目】如图,直线y=kx(k<0)与双曲线![]() 交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.
交于A(x1,y1),B(x2,y2)两点,则3x1y2-5x2y1的值为 __________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解分式方程:
(1) ![]() (2)
(2) ![]()
【答案】(1) ![]() ;(2)x=
;(2)x=![]()
【解析】试题分析:(1)两边乘以(x-1)(2x+1)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可;
(2)两边乘以(x+2)(x-2)去分母,转化为整式方程,然后解整式方程,检验后写出分式方程的解即可.
试题解析:
解:(1)两边乘以(x-1)(2x+1)去分母得:2x+1=5(x-1),
解得:x=2,
当x=2时,(x-1)(2x+1)≠0,
∴原分式方程的解为x=2;
(2)两边乘以(x+2)(x-2)去分母得:(x-2)2-3=(x+2)(x-2),
解得:x=![]() ,
,
当x=![]() 时,(x+2)(x-2)≠0,
时,(x+2)(x-2)≠0,
所以原分式方程的解为x=![]() .
.
【题型】解答题
【结束】
21
【题目】先化简,再求值![]() ,其中
,其中![]() 的值从不等式组
的值从不等式组![]() 的整数解中选取.
的整数解中选取.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生课外阅读的喜好,某校从八年级随机抽取部分学生进行问卷调查,调查要求每人只选取一种喜欢的书籍,如果没有喜欢的书籍,则作“其它”类统计。图(1)与图(2)是整理数据后绘制的两幅不完整的统计图。以下结论不正确的是( )
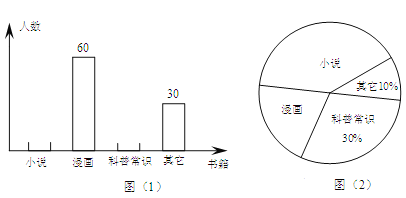
A. 由这两个统计图可知喜欢“科普常识”的学生有90人.
B. 若该年级共有1200名学生,则由这两个统计图可估计喜爱“科普常识”的学生约有360个.
C. 由这两个统计图不能确定喜欢“小说”的人数.
D. 在扇形统计图中,“漫画”所在扇形的圆心角为72°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( ) 
A.50°
B.51°
C.51.5°
D.52.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C 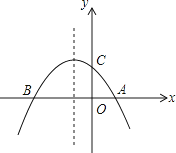
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若∠1=100°,∠4=80°,则__________,理由是________________;若∠3=70°,则∠2=_______时,也可推出AB∥CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com