
【题目】如图,若∠1=100°,∠4=80°,则__________,理由是________________;若∠3=70°,则∠2=_______时,也可推出AB∥CD.

【答案】 AB∥CD 同旁内角互补,两直线平行 110°
【解析】
因为∠1和∠4是直线AB和直线CD被第三条直线所截的同旁内角,且∠1+∠4=180°,根据同旁内角互补,两直线平行可得:AB//CD,又因为∠2和∠3是直线AB和直线CD被第三条直线所截的同旁内角,因为∠3=70°,根据两直线平行,同旁内角互补可得: ∠2=110°
因为∠1=100°,∠4=80°,
所以∠1+∠4=180°,
所以AB//CD(理由:同旁内角互补,两直线平行)
又因为∠2和∠3是直线AB和直线CD被第三条直线所截的同旁内角,且AB//CD,
所以∠2+∠3=180°,
因为∠3=70°,
所以∠2=110°.
故答案为: AB//CD, 同旁内角互补,两直线平行, 110°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线y=x2﹣x上,且﹣2≤h<1时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠B=∠C,AD∥BC.
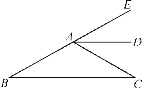
(1)证明:AD平分∠CAE;
(2)如果∠BAC=120°,求∠B的度数.(不允许使用三角形内角和为180°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com