
【题目】如图,已知抛物线y=﹣ ![]() x2﹣
x2﹣ ![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C 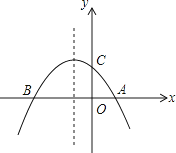
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:令y=0得﹣ ![]() x2﹣
x2﹣ ![]() x+2=0,
x+2=0,
∴x2+2x﹣8=0,
x=﹣4或2,
∴点A坐标(2,0),点B坐标(﹣4,0),
令x=0,得y=2,
∴点C坐标(0,2)
(2)
解:由图象可知AB只能为平行四边形的边,
∵AB=EF=6,对称轴x=﹣1,
∴点E的横坐标为﹣7或5,
∴点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣ ![]() ),此时点F(﹣1,﹣
),此时点F(﹣1,﹣ ![]() ),∴以A,B,E,F为顶点的平行四边形的面积=6×
),∴以A,B,E,F为顶点的平行四边形的面积=6× ![]() =
= ![]()
(3)
如图所示,
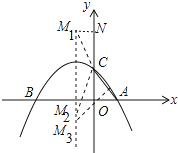
①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN= ![]() =
= ![]() ,
,
∴点M1坐标(﹣1,2+ ![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣ ![]() ).
).
②当M3为顶点时,∵直线AC解析式为y=﹣x+1,
线段AC的垂直平分线为y=x,
∴点M3坐标为(﹣1,﹣1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+ ![]() )或(﹣1.2﹣
)或(﹣1.2﹣ ![]() ).
).
【解析】(1)分别令y=0,x=0,即可解决问题.(2)由图象可知AB只能为平行四边形的边,易知点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣ ![]() ),由此不难解决问题.(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识,解题的关键是熟练掌握抛物线与坐标轴交点的求法,学会分类讨论的思想,属于中考压轴题.
),由此不难解决问题.(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识,解题的关键是熟练掌握抛物线与坐标轴交点的求法,学会分类讨论的思想,属于中考压轴题.
【考点精析】根据题目的已知条件,利用勾股定理的概念和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】如图,点A在∠O的一边OA上.按要求画图并填空:
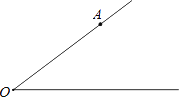
(1)过点A画直线AB⊥OA,与∠O的另一边相交于点B;过点A画OB的垂线段AC,垂足为点C;过点C画直线CD∥OA,交直线AB于点D。
(2)∠CDB=________°;
(3)如果OA=8,AB=6,OB=10,则点A到直线OB的距离为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动员在一场篮球比赛中的技术统计如表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 | 罚球得分 | 篮板 | 助攻(次) | 个人总得分 |
数据 | 46 | 66 | 22 | 10 | 11 | 8 | 60 |
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.不可能事件发生的概率为0
B.随机事件发生的概率为 ![]()
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;

2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线y=tx2(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线y=x2﹣x上,且﹣2≤h<1时,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com