
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)

【答案】(1)△ABP的周长为7+![]() ;
;
(2)当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形.
【解析】试题分析:(1)根据速度为每秒1cm,求出出发2秒后CP的长,然后就知AP的长,利用勾股定理求得PB的长,最后即可求得周长.
(2)因为AB与CB,由勾股定理得AC=4cm,因为AB为5cm,所以必须使AC=CB,或CB=AB,所以必须使AC或AB等于3,有两种情况,△BCP为等腰三角形.
试题解析:(1)如图1,由∠C=90°,AB=5cm,BC=3cm,
∴AC=4,动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,
∴出发2秒后,则CP=2,
∵∠C=90°,
∴PB=![]()
∴△ABP的周长为:AP+PB+AB=2+5+![]() =7+
=7+![]()
(2)①如图2,若P在边AC上时,BC=CP=3cm,
此时用的时间为3s,△BCP为等腰三角形;
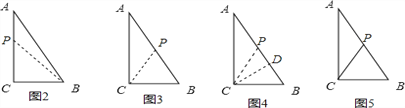
②若P在AB边上时,有三种情况:
i)如图3,若使BP=CB=3cm,此时AP=2cm,P运动的路程为2+4=6cm,
所以用的时间为6s,△BCP为等腰三角形;
ii)如图4,若CP=BC=3cm,过C作斜边AB的高,根据面积法求得高为2.4cm,
作CD⊥AB于点D,
在Rt△PCD中,PD=1.8,
所以BP=2PD=3.6cm,
所以P运动的路程为9-3.6=5.4cm,
则用的时间为5.4s,△BCP为等腰三角形;
ⅲ)如图5,若BP=CP,此时P应该为斜边AB的中点,P运动的路程为4+2.5=6.5cm
则所用的时间为6.5s,△BCP为等腰三角形;
综上所述,当t为3s、5.4s、6s、6.5s时,△BCP为等腰三角形


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】小明将父亲经营的便利店中“收入100元”记作“+100元”,那么“﹣80元”表示( )
A. 支出20元 B. 支出80元 C. 收入20元 D. 收入80元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
①射线AB和射线BA是同一条射线;
②若AB=BC,则点B为线段AC的中点;
③同角的补角相等;
④点C在线段AB上,M,N分别是线段AC,CB的中点.若MN=5,则线段AB=10.
A.①②
B.②③
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
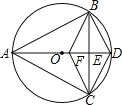
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°.
(1)作∠B的平分线BD,交AC于点D;
(2)作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(3)连接DE,求证:△ADE≌△BDE.
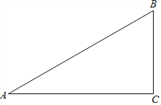
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列按一定规律排列的三行数:
1,-2,4,-8,16,-32,64,···;①
4, 1, 7,-5,19,-29,67,···; ②
-2,1,-5,7,-17,31,-65···; ③
(1)第①行数的第10个数是________;
(2)第②行数的第n个数是________;
(3)取每行数的第m个数,是否存在m的值,使这三个数的和等于1026?若存在,求出m的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com