Question

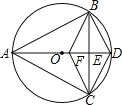
【题目】如图，已知△ABC内接于⊙O，且AB=AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD．

（1）求证：BE=CE；

（2）试判断四边形BFCD的形状，并说明理由；

（3）若BC=8，AD=10，求CD的长．

Answer 1

【答案】(1)、证明过程见解析；(2)、菱形；理由见解析；(3)、2

【解析】

试题分析：(1)、根据直径得出∠ABD=∠ACD=90°，从而的得出Rt△ABD≌Rt△ACD，然后得出答案；(2)、首先证明△BED≌△CEF，得出CF=BD，即四边形BFCD是平行四边形，根据BD=CD得出菱形；(3)、根据AD是直径，AD⊥BC，BE=CE得出CE2=DEAE，设DE=x，然后求出x的值，根据Rt△CED的勾股定理得出CD的长度.

试题解析：(1)、∵AD是直径， ∴∠ABD=∠ACD=90°，

在Rt△ABD和Rt△ACD中，∴Rt△ABD≌Rt△ACD， ∴∠BAD=∠CAD，∵AB=AC，∴BE=CE

(2)、四边形BFCD是菱形．

∵AD是直径，AB=AC，∴AD⊥BC，BE=CE， ∵CF∥BD，∴∠FCE=∠DBE，

在△BED和△CEF中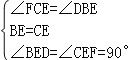， ∴△BED≌△CEF，∴CF=BD， ∴四边形BFCD是平行四边形，

∵∠BAD=∠CAD，∴BD=CD， ∴四边形BFCD是菱形

(3)、∵AD是直径，AD⊥BC，BE=CE， ∴CE2=DEAE，设DE=x，∵BC=8，AD=10，∴42=x（10﹣x），

解得：x=2或x=8（舍去） 在Rt△CED中，CD===2．