
����Ŀ��ij��˾�ɳ��׳�ǰ��ij���������ʱ����һ���������ͳ�����ͬʱ����������ͬһ����·��������ʻ���ٶȱ��ֲ��䣩��Ϊ��ȷ��������λ�ã�������OX��ʾ������·��ԭ��OΪ��ǧ��·�꣬��������Լ�����ٶ�Ϊ������ʾ�������������������ʻ���ٶ�Ϊ������ʾ����������ĸ�������ʻ���ٶ�Ϊ�㣬��ʾ������ֹ���г�Ϊ������ʾ����λ����ǧ���Ҳࣻ�г�Ϊ������ʾ����λ����ǧ����ࣻ�г�Ϊ�㣬��ʾ����λ����ǧ�״��������г̼�¼�����

����������е����ݣ�����������⣺
��1���׳�����7Сʱʱ��λ��Ϊ�� ��km���������ͳ�����λ��Ϊ�� ��km��
��2��������ͬʱ����xСʱʱ���׳�λ��Ϊ�� ��km���������ͳ�λ��Ϊ�� �� km ����x�Ĵ���ʽ��ʾ����
��3���׳�����ǰ����δ���ͣ�����������˾���ŷ������������ͽ�����ʻ3Сʱ���ʣ��׳�������ʻ3Сʱ���ܷ����̻���������ͳ��İ�������˵�����ɣ�
���𰸡���1����90����80��
��2��190��40x����80+50x��
��3���׳������̻���������ͳ��İ�����
�������������������1�����ݼ׳���λ�ú�ʱ������׳����ٶȣ�����ԭ����λ�ü�ȥ7Сʱ�Ժ��λ�ã���������׳�����7Сʱʱ��λ�ã�����5Сʱ��������λ�ú�7Сʱ��λ��������������ٶȣ��ٸ���·��=�ٶȡ�ʱ�䣬���ɵó��𰸣���2�����ݣ�1��������ٶȵó�xСʱ���·�̣�����ԭλ�ü�ȥ���ڵ�λ�ü��ɵó��׳���λ�ã��ã�1��������������ٶȳ���ʱ��������ڵ�λ�ã��ټ���������ԭ����λ�ü��ɵó��𰸣���3���ȼ��������3Сʱ�׳���λ�ú��������ͳ���λ�ã����߱Ƚϼ��ɵó��𰸣�
���������
��1����������ã�
�׳�����7Сʱʱ��λ��Ϊ��190-7����200��5��=-90��km����
�������ͳ�����λ��Ϊ��270-��270-170����2��7=-80��km����
�ʴ�Ϊ����90����80��
��2����������ã�
������ͬʱ����xСʱʱ���׳�λ��Ϊ��190��40x��
�������ͳ�λ��Ϊ����80+50x��
��3����x=3ʱ���׳�������λ���ǣ�190��40x=70��km����
�������ͳ���λ���ǣ���80+50x=70��km����
��׳������̻���������ͳ��İ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ����ǿѧ�����ʣ�����������������������Ŀ��A������ B��ƹ����C����ë�� D������Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ�������ȡ�˲���ѧ�����е��飬�������������Ƴ���������������ͳ��ͼ��

��ش��������⣺
��1����α������ѧ�����ж����ˣ�
��2�����㽫����ͳ��ͼ��2������������
��3����ƽʱ��ƹ������Ŀѵ���У��ס��ҡ����������˱������㣬�־�����������ͬѧ����ѡ�����μ�ƹ�����������ǡ��ѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ���б������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������Ӫ�ı�������������100Ԫ��������+100Ԫ������ô����80Ԫ����ʾ��������
A. ֧��20Ԫ B. ֧��80Ԫ C. ����20Ԫ D. ����80Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC����A��B��C���У�AB=A��B�䣬��B=��B���������������Բ�һ���ܱ�֤��ABC�ա�A��B��C���������������ǣ� ��

A. BC=B��C�� B. ��A=��A�� C. AC=A��C�� D. ��C=��C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬BC=1��AC=2���ѱ߳��ֱ�Ϊx1��x2��x3������xn��n�����������η��� ��ABC�У���ش��������⣺
��1����Ҫ�������
n | 1 | 2 | 3 |
xn |
��2����n�������εı߳�xn= ��
��3����m��n��p��q������������xmxn=xpxq�����ж�m��n��p��q�Ĺ�ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2��ͼ������ƽ��3����λ���õ��µ�ͼ��ĺ�������ʽ�ǣ� ��
A.y=x2+3
B.y=x2��3
C.y=��x+3��2
D.y=��x��3��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���ǣ�������
������AB������BA��ͬһ�����ߣ�
����AB=BC�����BΪ�߶�AC���е㣻
��ͬ�ǵIJ�����ȣ�
�ܵ�C���߶�AB�ϣ�M��N�ֱ����߶�AC��CB���е㣮��MN=5�����߶�AB=10��
A.�٢�
B.�ڢ�
C.�ڢ�
D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
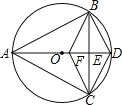
����Ŀ����ͼ����֪��ABC�ڽ�����O����AB=AC��ֱ��AD��BC�ڵ�E��F��OE�ϵ�һ�㣬ʹCF��BD��
��1����֤��BE=CE��
��2�����ж��ı���BFCD����״����˵�����ɣ�
��3����BC=8��AD=10����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����а�һ���������е���������
1����2��4����8��16����32��64������������
4�� 1�� 7����5��19����29��67���������� ��
��2��1����5��7����17��31����65�������� ��
��1���ڢ������ĵ�10������________��
��2���ڢ������ĵ�n������________��
��3��ȡÿ�����ĵ�m�������Ƿ����m��ֵ��ʹ���������ĺ͵���1026�������ڣ����m��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com