
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
分析 求M与N的大小,只要把M与N作差即可,看最终的结果即可解答本题.
解答 解:∵a>b>c,设M=$\frac{2}{a-c}$,N=$\frac{1}{a-b}$+$\frac{1}{b-c}$,
∴M-N
=$\frac{2}{a-c}-(\frac{1}{a-b}+\frac{1}{b-c})$
=$\frac{2}{a-c}-\frac{1}{a-b}-\frac{1}{b-c}$
=$\frac{2(a-b)(b-c)-(a-c)(b-c)-(a-c)(a-b)}{(a-c)(a-b)(b-c)}$
=$\frac{(b-c)[(a-b)-(a-c)]+(a-b)[(b-c)-(a-c)]}{(a-c)(a-b)(b-c)}$
=$\frac{-(b-c)^{2}-(a-b)^{2}}{(a-c)(a-b)(b-c)}$
∵a>b>c,
∴a-c>0,a-b>0,b-c>0,-(b-c)2<0,-(a-b)2<0,
∴$\frac{-(b-c)^{2}-(a-b)^{2}}{(a-c)(a-b)(b-c)}$<0,
∴M-N<0,
即M<N.
故选C.
点评 本题考查分式的加减法,解题的关键是M与N作差之后,由a>b>c,可以判断M与N的大小.


科目:初中数学 来源: 题型:解答题
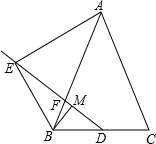 如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.
如图,已知在△ABC中AB=AC,点D为BC边的中点,点F在边AB上,点E在线段DF的延长线上,且∠BAE=∠BDF,点M在线段DF上,且∠EBM=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,1) | B. | (2,7) | C. | (5,4) | D. | (-1,4) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.45×106m2 | B. | 145×103m2 | C. | 1.45×104m2 | D. | 14.5×104m2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com