
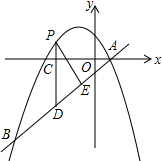
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{3}{4}$x-$\frac{3}{2}$��������y=-$\frac{1}{4}$x2+bx+c����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ-8��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{3}{4}$x-$\frac{3}{2}$��������y=-$\frac{1}{4}$x2+bx+c����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ-8������ ��1������ֱ�߽���ʽ�����A��B�����꣬�����ô���ϵ��������κ�������ʽ���
��2������ֱ�߽���ʽ�������߽���ʽ��ʾ��PD��������ͬ�ǵ������������DPE=��BAO������ֱ��kֵ�����BAO�����Һ�����ֵ��Ȼ���ʾ��PE��DE���ٸ��������ε��ܳ���ʽ��ʽ�������ɵý⣬�ٸ��ݶ��κ�������ֵ������
��� �⣺��1����y=0����$\frac{3}{4}$x-$\frac{3}{2}$=0�����x=2��
x=-8ʱ��y=$\frac{3}{4}$����-8��-$\frac{3}{2}$=-$\frac{15}{2}$��
���A��2��0����B��-8��-$\frac{15}{2}$����
�ѵ�A��B���������ߵ�$\left\{\begin{array}{l}{-\frac{1}{4}��{2}^{2}+2b+c=0}\\{-\frac{1}{4}����-8��^{2}-8b+c=-\frac{15}{2}}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=\frac{5}{2}}\end{array}\right.$��
�������ߵĽ���ʽy=-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$��
��2���ߵ�P���������ϣ���D��ֱ���ϣ�
��P��������x��-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$����D��������x��$\frac{3}{4}$x-$\frac{3}{2}$����
�ߵ�P��ֱ��AB�Ϸ�����������һ����
��PD=-$\frac{1}{4}$x2-$\frac{3}{4}$x+$\frac{5}{2}$-��$\frac{3}{4}$x-$\frac{3}{2}$��=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4��
��PE��AB��
���DPE+��PDE=90�㣬
�֡�PD��x�ᣬ
���BAO+��PDE=90�㣬
���DPE=��BAO��
��D��ֱ��AB�ϣ�
��$\frac{DC}{AC}$=$\frac{3}{4}$��
��sin��BAO=$\frac{3}{5}$��cos��BAO=$\frac{4}{5}$��
��PE=PDcos��DPE=$\frac{4}{5}$PD��
DE=PDsin��DPE=$\frac{3}{5}$PD��
���PDE���ܳ�Ϊl=PD+$\frac{4}{5}$PD+$\frac{3}{5}$PD=$\frac{12}{5}$PD=$\frac{12}{5}$��-$\frac{1}{4}$x2-$\frac{3}{2}$x+4-��=-$\frac{3}{5}$x2-$\frac{18}{5}$x+$\frac{48}{5}$��
��l=-$\frac{3}{5}$x2-$\frac{18}{5}$x+$\frac{48}{5}$��
��l=-$\frac{3}{5}$x2-$\frac{18}{5}$x+$\frac{48}{5}$=-$\frac{3}{5}$��x+3��2+15��
�൱x=-3ʱ��l���ֵΪ15��
���� ������Ҫ�����˶��κ������ۺ�Ӧ�ã�ȫ�������ε��ж��������Լ�����ϵ��������κ�������ʽ��������Ǻ�����Ӧ�ã���2������������Ǻ�����PD��ʾ�����������ܳ��ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
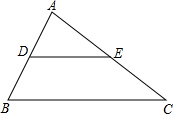 ��ͼ���ڡ�ABC�У�DE��BC����S��ADE��S�ı���BCED=1��2��BC=26����DE�ij���
��ͼ���ڡ�ABC�У�DE��BC����S��ADE��S�ı���BCED=1��2��BC=26����DE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6cm | B�� | 7cm | C�� | 8cm | D�� | 9cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com