
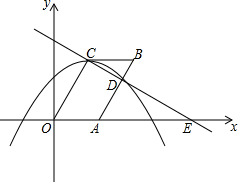
 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.分析 (1)由抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,可求得点C的坐标,继而求得线段OC的长,然后由三角函数的性质,可求得tan∠AOC=$\sqrt{3}$,继而求得∠AOC的度数;
(2)易证得△BCD∽△AED,然后由相似三角形的性质,求得点D的纵坐标,再代入抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$,即可求得答案;
(3)首先过点D作DG⊥x轴于点G,易证得△DGE∽△CFE,△BCD∽△OEC,然后由相似三角形的性质,求得点E与点A的坐标,再由勾股定理的逆定理证得AD⊥CD,求得AD=OA,即可判定以点A为圆心,AO长为半径的圆与直线CD相切.
解答 解:(1)过点C作CF⊥OA于点F,
∵抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,
∴点C的坐标为:($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$),
∴OF=$\frac{3}{2}$,CF=$\frac{3\sqrt{3}}{2}$,
∴OC$\sqrt{O{F}^{2}+C{F}^{2}}$=$\sqrt{(\frac{3}{2})^{2}+(\frac{3\sqrt{3}}{2})^{2}}$=3,
∵tan∠AOC=$\frac{CF}{OF}$=$\frac{\frac{3\sqrt{3}}{2}}{\frac{3}{2}}$=$\sqrt{3}$,
∴∠AOC=60°;
(2)根据平移的性质可得:B的纵坐标为$\frac{3\sqrt{3}}{2}$,且BC∥OA,
∴△BCD∽△AED,
∴$\frac{BC}{AE}=\frac{CD}{DE}$=$\frac{BD}{AD}$=$\frac{1}{2}$,
∴点D的纵坐标为:$\frac{3\sqrt{3}}{2}$×$\frac{2}{3}$=$\sqrt{3}$,
将y=$\sqrt{3}$代入y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$,
解得:x1=3,x2=0(舍去),
∴点D的坐标为:(3,$\sqrt{3}$);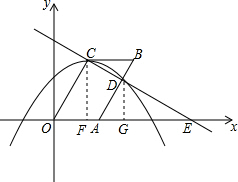
(3)相切.
理由:过点D作DG⊥x轴于点G,
∴DG∥CF,
∴△DGE∽△CFE,
∴EG:EF=ED:EC=2:3,
∵OG=3,OF=$\frac{3}{2}$,
∴FG=$\frac{3}{2}$,
∴EG=2FG=3,
∴OE=OG+EG=6,
∵∠AOC=∠B,∠OEC=∠BCD,
∴△BCD∽△OEC,
∴BC:OE=BD:OC=1:3,
∴BC=2,
∴OA=BC=2,
∴AD=$\sqrt{({3-2)}^{2}+(\sqrt{3})^{2}}$=2,DE=$\sqrt{(6-3)^{2}+({\sqrt{3})}^{2}}$=2$\sqrt{3}$,AE=4,
∴AD2+DE2=AE2,
∴∠ADE=90°,
即AD⊥DE,
∵AD=OA=2,
∴以点A为圆心,AO长为半径的圆与直线CD相切.
点评 此题属于二次函数的综合题,考查了抛物线的性质、相似三角形的判定与性质、平行四边形的性质以及勾股定理的逆定理.注意准确作出辅助线是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
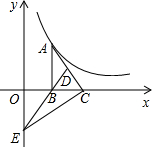 如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.
如图,Rt△ABC的直角边BC在x轴正半轴上,点D为斜边AC上一点,AD=2CD,DB的延长线交y轴于点E,函数y=$\frac{k}{x}$(k>0)的图象经过点A,若S△BCE=2,则k=8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
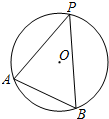 如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
如图,A,B,P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com