
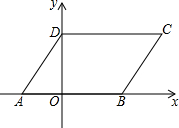
 如图,ABCD是平行四边形,AD=4,AB=5,A坐标为(-2,0),在图上标出其它各顶点的坐标.
如图,ABCD是平行四边形,AD=4,AB=5,A坐标为(-2,0),在图上标出其它各顶点的坐标. 分析 由A坐标为(-2,0),可求得OA的长,又由AD=4,AB=5,即可求得点B与点D的坐标,继而求得点C的坐标.
解答 解:∵A坐标为(-2,0),
∴OA=2,
∵AD=4,AB=5,
∴OB=AB-OA=3,OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=2$\sqrt{3}$,
∴点B(3,0),点D(0,2$\sqrt{3}$),
∵四边形ABCD是平行四边形,
∴CD=AB,
∴点C(5,2$\sqrt{3}$).
即B(3,0),C(5,2$\sqrt{3}$),D(0,2$\sqrt{3}$).
点评 此题考查了平行四边形的性质以及勾股定理.注意坐标与图形的关系.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
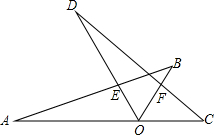 如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
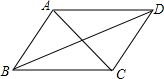 如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是②③.(填序号)
如图,在下列条件中:①∠DAC=∠ACB;②∠BAC=∠ACD;③∠BAD+∠ADC=180°;④∠BAD+∠ABC=180°.其中能使直线AB∥CD成立的是②③.(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
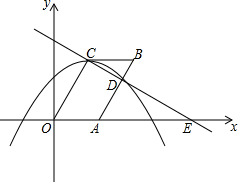 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{2\sqrt{3}}{9}$(x-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{2}$的顶点为C,连结OC,将线段OC沿x轴的正方向平移到AB交已知抛物线于点D,直线CD交x轴于点E,连结BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com